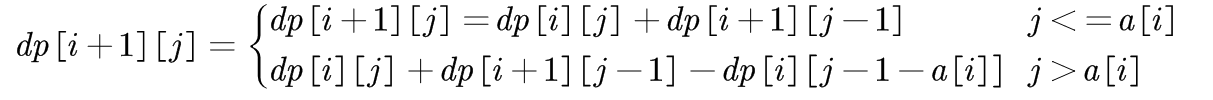题目描述
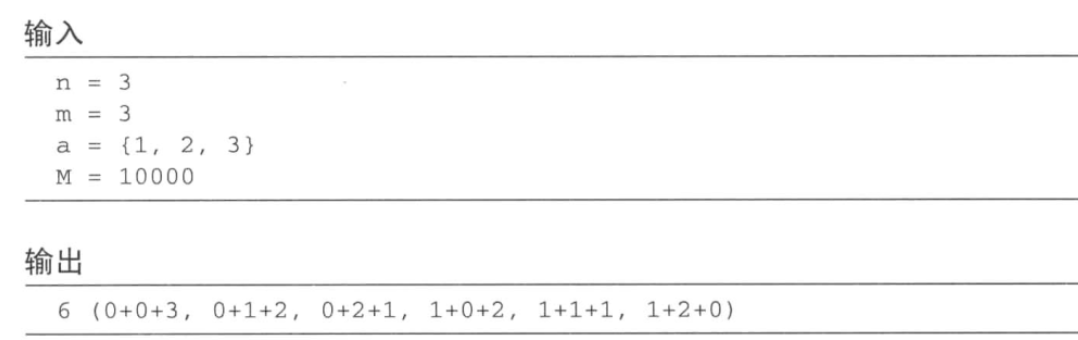
有 n 种物品，第 i 种物品有 a_i 个，不同种类的物品可以互相区分, 但相同种类的无法区分。从这些物品中取出 m 个, 有多少种取法? 求出数模 M 的余数.：
解析
考虑使用动态规划方法进行实现，定义状态方程为：dp[i][j]=前 i 类物品中取出 j 个的组合总数。可以得到以下状态转移方程：
以上递推公式包含三层循环，时间复杂度为 O(n*m^2)，显然是过高了，于是我们考虑进行优化：
首先分为两种情况进行讨论：
1）j<=a[i]，即(j-1<a[i])时：原式可以展开为 dp[i+1][j]=dp[i][j]+dp[i][j-1]+···+dp[i][0]，可以注意到 dp[i+1][j-1]=dp[i][j-1]+···+dp[i][0]，因此有 dp[i+1][j]=dp[i][j]+dp[i+1][j-1]。
2）j>a[i]时：原式可以展开为 dp[i+1][j]=dp[i][j]+dp[i][j-1]+···+dp[i][j-a[i]]，注意到 dp[i+1][j-1]=dp[i][j-1]+···+dp[i][j-a[i]-1]，因此 dp[i+1][j]=dp[i][j]+dp[i+1][j-1]-dp[i][j-a[i]-1]。
综上，我们可以得到以下状态转移方程：
代码实现（C++）
#include<bits/stdc++.h>
using namespace std;
int n,m,M;
int a[1001];
int dp[1001][1001];
int main(){
cin>>n>>m>>M;
for(int i = 0;i < n;i++){
cin>>a[i];
}
for(int i = 0; i <= n; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
for(int j = 1; j <= m; j++){
if(j - 1 - a[i] >= 0){
dp[i + 1][j] = (dp[i][j] + dp[i + 1][j - 1] - dp[i][j - 1 - a[i]] + M) % M;
}else{
dp[i + 1][j] = (dp[i][j] + dp[i + 1][j - 1]) % M;
}
}
}
cout<<"解为："<<dp[n][m]<<endl;
return 0;
}
