需要使用的 Matlab 函数
clc,clear %%清理工作空间,清除变量 unifrnd(a,b,[c,d]):生成 c 行 d 列的随机数矩阵,矩阵范围在 a~b 之间 使用 function 定义函数: function[输出内容] = 函数名(输入值) %%函数内容定义 end rand(‘state’,sum(clock)) %%根据当前时间定义 randi([a,b],c,d) %%返回一个 a 行 b 列的随机数矩阵,随机数值在 c 到 d 之间 c(:) %%将矩阵化为列矩阵 zeros(a,b) %%获得一个全为 0 的 a 行 b 列矩阵 ones(a,b) %%获得一个全为 1 的 a 行 b 列矩阵 reshape(x,[a,b]) %%将 x 转化为一个 a 行 b 列的矩阵
使用 Matlab 实现蒙特卡洛法求解整数规划
蒙特卡洛法是一种基于随机取样的求解方法,是一种枚举法。其每次运算得出的结果都有可能不同,大多数情况下获得的都是满意解,难以取得最优解。
求解非线性整数规划的 Matlab 程序如下:
clc,clear
function[f,g] = mengte(x) %%输入 x 的整数向量,返回目标值和约束向量
f = ; %%定义目标函数
g = []; %%定义约束向量
end
rand('state',sum(clock));
f_ans = 0;
x_ans = zeros(3,1);
for i = 1 : 10^6 %%循环 10^6 次
x = ; %%根据约束条件生成随机的 x 向量
[f,g] = mengte(x);
if all(g < 0) %%判断符合约束条件的条件
if(f > ans) %%判断是否出现了更优值
f_ans = f;
x_ans = x;
end
end
end
x_ans,f_ans
Lingo 求解整数规划
Lingo 可以直接求得全局最优解:
model: sets: row/1..4/:b; col/1..5/:c1,c2,x; link(row,col):a; endset data: c1 = ; c2 = ; a = ; b = ; endata max = ; %%定义目标函数 @for (row(i): @sum(col(j): a(i,j) * x(j) < b(i)); %%定义约束条件 @for (col: @gin(x)); %%约束 x 为整数 @for (col: @bnd(a, x, b)); %%约束 x 的值在 a 和 b 之间
Matlab 求解整数线性规划
在 Matlab 中求解整数线性规划一般使用 intlinprog 函数进行求解,函数表达式为:
[x,fval] = intlinprog(f,intcon,A,b,AEQ,beq,lb,ub)
其中 intcon 规定那些变量取整数,如 intcon = 1:25 指 x1~x25 均为整数。
但是其只能求解一维决策变量,因此在面对多维决策变量时应该将其化为一维变量进行求解。
在 Matlab 中,线性整数规划的标准型如下:
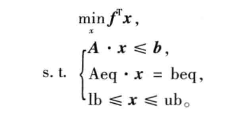
其中 x 均整数


