1.4 一架货机有三个货舱:前舱、中仓和后舱
三个货舱所能装载的货物的最大重量和体积有限制如表 1.3 所列。并且为了飞机的平衡,三个货舱装载的货物重量必须与其最大的容许量成比例。

现有四类货物用该货机进行装运,货物的规格以及装运后获得的利润如表 1.4 所列。
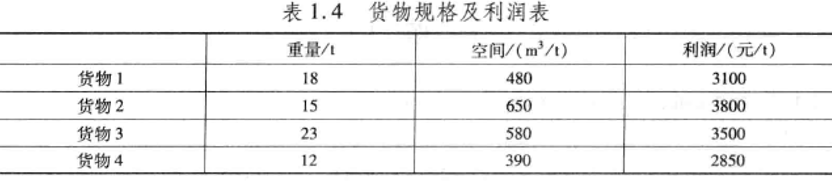
假设:
(1)每种货物可以无限细分:
(2)每种货物可以分布在一个或者多个货舱内:
(3)不同的货物可以放在同一个货舱内,并且可以保证不留空隙。
问应如何装运,能使货机飞行利润最大?
解答:
记货物 1..4 的 x1、x2、x3、x4 放置在前舱;记货物 1..4 的 x5、x6、x7、x8 放置在前舱;记货物 1..4 的 x9、x10、x11、x12 放置在前舱;
由题可建立线性规划模型:
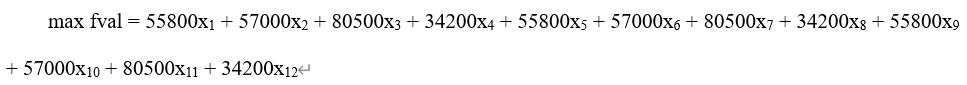

根据线性规划模型,得到模型解题的Matlab 语句:
>> f = [-55800; -57000; -80500; -34200; -55800; -57000; -80500; -34200; -55800; -57000; -80500; -34200]; >> a = [18, 15, 23, 12, 0, 0, 0, 0, 0, 0, 0, 0; 0, 0, 0, 0, 18, 15, 23, 12, 0, 0, 0, 0; 0, 0, 0, 0, 0, 0, 0, 0, 18, 15, 23, 12; 8640, 9750, 13340, 4680, 0, 0, 0, 0, 0, 0, 0, 0; 0, 0, 0, 0, 8640, 9750, 13340, 4680, 0, 0, 0, 0; 0, 0, 0, 0, 0, 0, 0, 0, 8640, 9750, 13340, 4680; 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0; 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0; 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0; 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1]; >> b = [10; 16; 8; 6800; 8700; 5300; 1; 1; 1; 1]; >> aeq = [144, 120, 184, 96, -90, -75, -115, -60, 0, 0, 0, 0; 72, 60, 92, 48, 0, 0, 0, 0, -90, -75, -115, -60; 0, 0, 0, 0, 18, 15, 23, 12, -36, -30, -46, -24]; >> beq = [0; 0; 0]; >> [x,fval] = linprog(f, a, b, aeq, beq, zeros(12, 1)); >> wu = [18 * (x(1) + x(5) + x(9)); 15 * (x(2) + x(6) + x(10)); 23 * (x(3) + x(7) + x(11)); 12 * (x(4) + x(8) + x(12))] %%各个货物的运送的数量 >> wv = [18 * x(1) + 15 * x(2) + 23 * x(3) + 12 * x(4); 18 * x(5) + 15 * x(6) + 23 * x(7) + 12 * x(8); 18 * x(9) + 15 * x(10) + 23 * x(11) + 12 * x(12)] %%各个仓的运送的数量 >> vu = [8640 * (x(1) + x(5) + x(9)); 9750 * (x(2) + x(6) + x(10)); 13340 * (x(3) + x(7) + x(11)); 4680 * (x(4) + x(8) + x(12))] %%各个货物的运送的空间 >> vv = [8640 * x(1) + 9750 * x(2) + 13340 * x(3) + 4680 * x(4); 8640 * x(5) + 9750 * x(6) + 13340 * x(7) + 4680 * x(8); 8640 * x(9) + 9750 * x(10) + 13340 * x(11) + 4680 * x(12)] %%各个仓的运送的空间 >> fval = -fval


