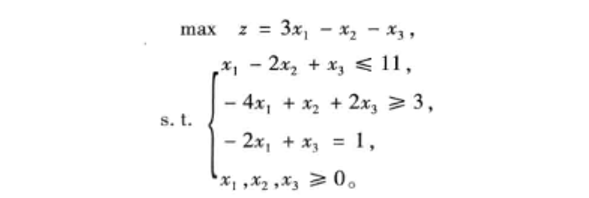1.1 分别用 Matlab 与 Lingo 求解下列线性规划问题
>> f = [-3; 1; 1]; >> a = [1, -2, 1; 4, -1, -2]; >> b = [11; -3]; >> aeq = [-2, 0, 1]; >> beq = [1]; >> [x,fval] = linprog(f, a, b, aeq, beq, zeros(3, 1)); >> x, fval = -fval
Lingo 语句:
model: sets: row/1..2/: b; col/1..3/: c, x, aeq; links(row, col): a; endsets data: c = 3 -1 -1; a = 1 -2 1 4 -1 -2; b = 11 -3; aeq = -2 0 1; enddata min = @sum(col:c*x); @for(row(i) : @sum(col(j) : a(i, j) * x(j) ) <= b(i)); @sum(col : aeq * x) = 1;
1.2 分别用 Matlab 与 Lingo 求解下列线性规划问题
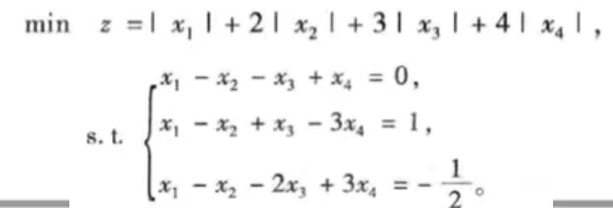
本题并不是一个标准的线性规划模型,需要先进行一些变形,记 ui = (xi + |xi|)/2 , vi = (xi – |xi|)/2。
得到Matlab 语句:
>> f = [1; 2; 3; 4; 1; 2; 3; 4]; >> aeq = [1, -1, -1, 1, 1, -1, -1, 1; 1, -1, 1, -3, 1, -1, 1, -3; 1, -1, -2, 3, 1, -1, -2, 3]; >> beq = [0; 1; -0.5]; >> [u,fval] = linprog(f, [], [], aeq, beq, zeros(8, 1)); >> x = [u(1) + u(5); u(2) + u(6); u(3) + u(7); u(4) + u(8);] >> fval = -fval
以及Lingo 语句:
model: sets: row/1..3/: b; col/1..8/: c, x, aeq; links(row, col): a; endsets data: c = 1 2 3 4; a = 1 -1 -1 1 1 -1 -1 1 1 -1 1 -3 1 -1 1 -3 1 -1 -2 3 1 -1 -2 3; b = 0 1 -0.5; enddata min = @sum(col:c*x); @for(row(i) : @sum(col(j) : a(i, j) * x(j) ) = b(i));