Matlab 求解线性规划的代码模板:
在 Matlab 中,线性规划的标准型如下:
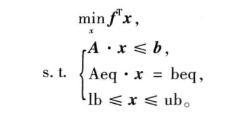
Matlab 中求解线性规划问题的函数为 linprog,其各项参数如下:

其中:
x 为决策向量;fval 是最优解;f 为价值系数;
A 和 b 为线性不等式约束;Aeq 和 beq 为线性等式约束;
lb 和 ub 分别为决策向量的下界向量和上界向量;
若求解得到的 x 是一个矩阵,需要在每条语句后面加上 zeros(m,n) 用来表示 x 的结果;
根据以上内容,列出在Matlab中的源代码模板为:
>> f = [ ; ; ]; >> a = [ , , ; , , ]; >> b = [ ; ]; >> aeq = [ , , ]; >> beq = [ ]; >> [x,fval] = linprog(f, a, b, aeq, beq, zeros( , )); >> x, fval = -fval
Lingo 求解线性规划的代码模板:
lingo 的常用函数(lingo 每个函数都必须用@强调):
!max, min 用于用于定义目标函数
@bin(x)表示 x 为 0 或 1
@gin(x)表示 x 是整数
@free(x)表示 x 为任意实数,因为变量默认为非负实数,所以必须用这个函数解除这种限制
@bnd(1, x, u)表示 x 为[1, u]之间的实数
如表示 x 在(-5,5)之间的整数,@free(x),@gin(x),@bnd(-5, x, 5)
根据以上内容,列出在Lingo中的源代码模板为:
model: !模型开始 sets: !定义集合; row/1..n/: b; !S 集合下标范围是 1 到 n,a b d 这三个变量用到了这个集合; col/1..m/: c, x; links(row, col): a; !双索引的集合,a 用到了这个集合; endsets !结束集合的定义; data: !定义已知变量,也就是为每个已知变量赋值; c = 1 2 3; !用空格进行间隔 a = 1 2 3; b = 1 2 3; enddata !结束数据的写入; !目标函数 min=@sum(col:c*x); !约束条件 @for(row(i):@sum(col(j):a(i,j)*x(j))<=b(i)); !其他形式可通过变形实现


