855学习记录算法动态规划$Day$-$7$——炎泽汐$de$ Blog

最优二叉搜索树

---

//最优二叉搜索树
double dp[MaxN + 1][MaxN + 1], w[MaxN + 1][MaxN + 1];
int s[MaxN + 1][MaxN + 1];
double OptimalBinarySearchTree(vector<double>& p, vector<double>& q){
    int n = p.size();
    memset(dp, 0, sizeof(dp));
    memset(w, 0, sizeof(w));
    memset(s, 0, sizeof(s));
    //初始化只包括虚拟键的子树
    for(int i = 0;i <= n; i++){
        w[i + 1][i] = q[i];
    }
	
    for(int len = 1; len <= n; len++){
        for(int i = 1; i + len - 1 <= n; i++){
            int l = i, r = i + len - 1;
            w[l][r] = w[l][r - 1] + p[r] + q[r];
            dp[l][r] = dp[l][l - 1] + dp[l + 1][r];
            s[l][r] = l;
            //选择根节点 
            for(int k = l + 1, k < r; k++){
                double t = dp[l][k - 1] + dp[k + 1][r];
                if(t < dp[l][k] && fabs(t - dp[i][j]) > 1E-6){
                    dp[l][k] = t;
                    s[l][k] = k;
                }
            }
            dp[l][r] += w[l][r];
        }
    }
}

最大连续子序列和

---

//最大连续子序列和 
int maxSubArray(vector<int>& nums) {
    int n = nums.size(), ans = nums[0]];
    int dp[n + 1];
    dp[0] = 0;
    
    for(int i = 1; i < n; i++){
    	dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
    	if(d[i] > ans){
            ans = dp[i];
        }
    }
	
    return ans;
}

//在线算法 
int maxSubArray(vector<int>& nums) {
    int ans = nums[0],sum = 0,n = nums.size();
    
    for(int i = 0;i < n;i++){
        sum += nums[i];
        if(sum > ans){
            ans = sum;
        }
        if(sum < 0){
            sum = 0;
        }
    }
    return ans;
}

最长回文子串

---

string longestPalindrome(string s) {
    int n = s.size(), max = 1, a = 0, b = 0;
    int dp[n][n];
    memset(dp, 0, sizeof(dp));
    for(int i = 0; i < n; i++){
        dp[i][i] = 1;
    }
    for(int L = 2; L <= n; L++){
        for(int i = 0; i + L - 1 < n; i++){
            int j = i + L - 1;
            if(s[i] == s[j] && (j - i == 1 || dp[i + 1][j - 1] == 1)){
                dp[i][j] = 1;
                dp[j][i] = 1;
                if(max < j - i + 1){
                    a = i;
                    b = j;
                    max = j - i + 1;
                }
            }
        }
    }
    string ans = s.substr(a, b - a + 1);
    return ans;
}

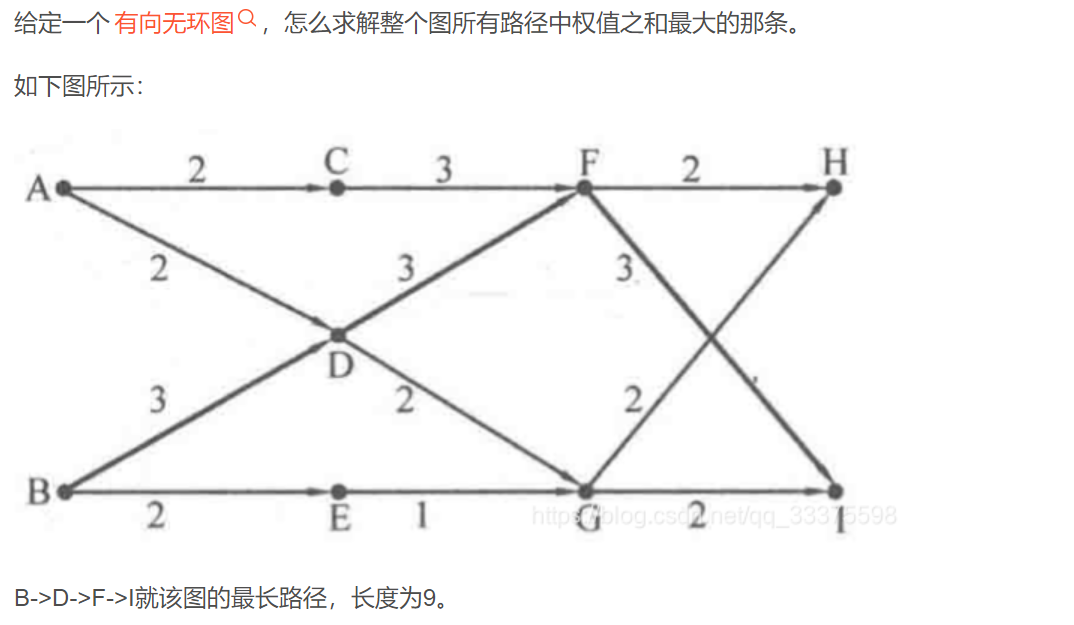
$DAG$最长路

---

//DAG 最长路 
//默认起始点为 0
const int inf = 0x3f3f;
int dp[MaxN];
memset(dp, 0, sizeof(dp));

int DAG(vector<vector<int> >& nums, int i){
    int n = nums.size();
    if(dp[i] > 0){
        return dp[i];
    }
	
    for(int j = 0; j < n; j++){
        if(num[i][j] != inf){
            int temp = DAG(nums, j) + num[i][j];
            if(temp > dp[i]){
                dp[i] = temp;
            }
        }
    }
	
    return dp[i];
}