855学习记录算法动态规划$Day$-$5$——炎泽汐$de$ Blog

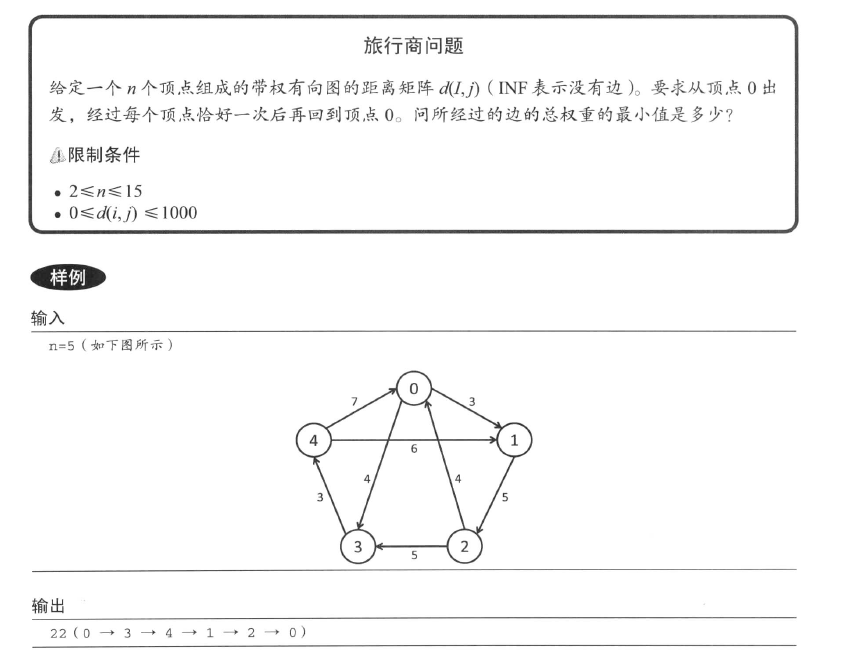
旅行商问题

---

//旅行商问题
//dp[S][v]表示在 S 已被访问时从 v 出发访问的最小值
//递归版 
int n;
vector<vector<int> > d;
int dp[1 << MaxN][MaxN];
memset(dp, -1, sizeof(dp));

int TSP(int S, int v){
    if(dp[S][v] >= 0){
        return dp[S][v];
    }
	
    if(S == (1 << n) - 1 && v == 0){
        return dp[S][v] = 0;
    }
	
    int res = 0x3f3f3f3f;
	
    for(int u = 0; u < n; u++){
        if(!(S >> u & 1)){
            res = min(res, TSP((S | (1 << u)), u) + d[v][u])
        }
    }
	
    return dp[S][v] = res;
}

TSP(0, 0);

//循环版
int TSP(vector<vector<int> >& d){
    int n = d.size();
    int dp[1 << n][n];
    memset(dp, 0x3f3f3f3f, sizeof(dp));
    dp[(1 << n) - 1][0] = 0;
	
    for(int S = (1 << n) - 2; S >= 0; S--){
    	for(int v = 0; v < n; v++){
            for(int u = 0; u < n; u++){
                if(!(S >> u & 1)){
                    dp[S][v] = min(dp[S][v], dp[S | (1 << u)][u] + d[v][u]);
                }
            }
        }
    }
	
    return dp[0][0];
}

编辑距离

---

int minDistance(string word1, string word2) {
    int m = word1.size(),n = word2.size();
    int dp[m + 1][n + 1];
    dp[0][0] = 0;
    for(int i = 1;i <= m;i++){
        dp[i][0] = i;
    }
    for(int i = 1;i <= n;i++){
        dp[0][i] = i;
    }
    for(int i = 1;i <= m;i++){
        for(int j = 1;j <= n;j++){
            if(word1[i - 1] == word2[j - 1]){
                dp[i][j] = dp[i - 1][j - 1];
            }else{
                dp[i][j] = min(dp[i][j - 1], min(dp[i - 1][j], dp[i - 1][j - 1]));
                dp[i][j] = dp[i][j] + 1;
            }
        }
    }
    return dp[m][n];
}