本体论
在“玩具”领域，选择何种表示并不那么重要，很多表示都可以良好运作。但在复杂的领域，如网上购物或者在车流中驾驶，就需要更为通用和灵活的表示方法。如何创建这些表示？主要关注于许多不同领域中都会出现的一般性的概念，如事件、时间、对象、信念等。有时，表示这些抽象概念被称为本体论工程。
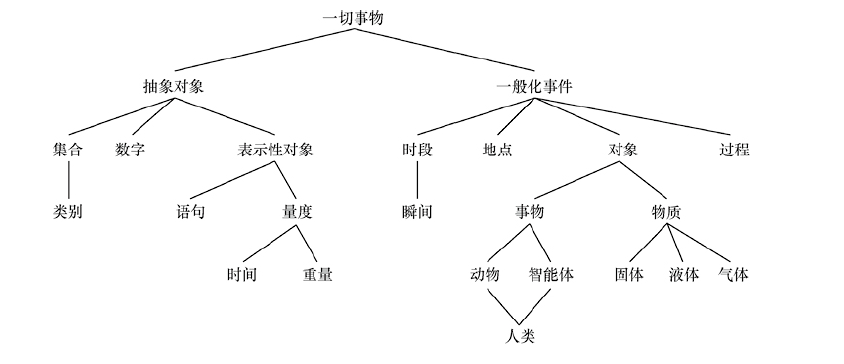
事实上表示世界中的一切事物是几乎不可能的，但通常会留出一些位置，使所有领域的新知识都可以填入。例如，定义对象是什么，而不同种类对象的细节——机器人、电视机、书或者无论什么——可以随后再进行填充补全。这类似于面向对象编程框架的设计者定义窗口之类的一般性概念，并期待用户使用它们来定义更为具体的概念，概念的一般性的框架被称为上层本体论，因为人们习惯于将更一般性的概念绘制于更具体的概念之上：
在进一步考虑本体论之前要先说明一项重要的提醒。尽管真实世界的一些层面很难用一阶逻辑来刻画，仍选择使用一阶逻辑来讨论知识的内容和组织。主要的难点在于，大多数一般化都有其例外，或仅在某种程度上成立。处理例外和不确定性的能力极其重要，但它却与理解一般性的本体论无关。
对所有专用本体论来说，通过修改来使其更为一般化是可行的。显然，这样做就产生了一个问题：这些本体论是否最终都会发展为通用本体论？在几个世纪的哲学和计算研究中，答案是“有可能”。通用本体论与专用本体论有两个主要的区别：
1、通用本体论在所有专用论域都应当可以或多或少地适用（在增加论域特定的公理后）。这意味着它不能无视任何表示问题。
2、在所有足够复杂的论域中，不同领域的知识必须是统一的，因为推理和问题求解会同时涉及多个领域。例如，一个机器人电路维修系统需要在电气连通性和物理布局方面推理电路，也需要出于电路时序分析和估计劳动力成本的目的而进行关于时间的推理。因此，描述时间的语句必须能够结合描述空间布局的语句，在处理纳秒或分钟、埃或米时也必须具有相同的性能。
目前为止，通用本体论工程的进展仍然相当有限。所有顶尖的人工智能应用都没有使用通用本体论——它们都使用专用知识工程和机器学习。对于争论各方，社会和政治考虑使得他们很难对某个本体论达成共识。如汤姆·格鲁伯所述：“每一种本体论都是一群有共同动机去分享的人之间的合约——社会共识。”当竞争方面的考虑超过共享时，就不会有共同的本体论。利益相关者的数量越少，就越容易构建本体论，因此构建通用本体论要难于构建用途有限的本体论，例如开放生物医学本体论。这些已有的本体论根据 4 条路径构建：
1、通过训练有素的本体论学家或逻辑学家团队来构建本体论并写出公理。
2、通过从现有数据库中引入类别、属性和值。
3、通过分析文本文件，从中提取信息。
4、通过诱导无技能的业余人士输入常识知识。
举例来说，谷歌知识图谱使用来自维基百科的半结构化内容，并结合了从大量网页中收集的、经过人类整合的内容。它含有超过 700 亿条事实并为大约三分之一的谷歌搜索提供答案。
经典规划
经典规划定义为在一个离散的、确定性的、静态的、完全可观测的环境中，找到完成目标的一系列动作的任务。前面已经见过两种完成这个任务的方法：搜索的问题求解智能体和逻辑的混合命题逻辑智能体。它们都受到两个限制。首先，对于每个新领域，它们都需要特定的启发式方法：用于搜索的启发式评价函数和用于混合$wumpus$智能体的人工代码。其次，它们都需要明确地表示指数量级的状态空间。
针对这些限制，规划研究者使用$PDDL$语言研究出了因子化表示。$PDDL$语言全称是规划领域定义语言，它利用单个动作模式可以表示$4Tn^2$个动作，且不需要特定的领域知识。基本的$PDDL$可以处理经典规划领域，而扩展的$PDDL$则可以处理连续的、部分可观测的、并发的和多智能体的非经典领域。$PDDL$的语法基于$Lisp$，但是这里将它转换成与$AIMA$中使用的表示法相符的形式。特别的，$PDDL$使用数据库语义。
一个动作模式表示一组基本动作。模式由动作名称、模式中使用的所有变量的列表、前提（$precondition$）和效果组成。前提和效果都是文字的合取（肯定或否定的原子句）。
如果状态$s$蕴含基本动作$a$的前提，也就是说，前提中的每一个正文字都在$s$中，且每一个负文字都不在$s$中，则动作$a$适用于状态$s$。在状态$s$中执行适用动作$a$的结果被定义为状态$s’$，状态$s’$的形成方式是从$s$出发，移除动作效果中以负文字形式出现的流，［称之为删除列表］，并添加在动作效果中以正文字形式出现的流［称之为添加列表］。
$$
\text{Re}sults\left( s,a \right) =\left( s \right) -Del\left( a \right) \cup Add\left( a \right)
$$
一组动作模式是规划领域的一个定义。领域中的特定问题是通过添加初始状态和目标来定义的。初始状态是基本流的合取。由于对所有状态都使用了封闭世界假设，这意味着任何没有被提及的原子都是假的。目标（使用$Goal$引入）和前提类似，它是可以含有变量的文字（正文字或负文字）合取式。
