所谓外部排序，即对外存中的记录进行排序（相对于内部排序而言）。有了内部排序算法，为什么还要外部排序?因为外存中记录规模太大，内存放不下。外部排序可以概括为一句话∶将内存作为工作空间来辅助外存数据的排序。外部排序最常用的算法是归并排序。归并排序之所以常用，是因为它不需要将全部记录都读入内存即可完成排序。因此，可以解决由于内存空间不足导致的无法对大规模记录排序的问题。
有了败者树，选出最小元素，只需对比关键字$\lceil \log _2k \rceil $次；
采用置换-选择排序算法构造初始归并段的过程∶根据缓冲区大小，由外存读入记录，当记录充满缓冲区后，选择最小的（假设升序排序）写回外存，其空缺位置由下一个读入记录来取代，输出的记录成为当前初始归并段的一部分。
如果新输入的记录不能成为当前生成的归并段的一部分，即它比生成的当前归并段中最大的记录要小，则它将成为生成其他初始归并段的选择。反复进行上述操作，直到缓冲区中的所有记录都比当前初始归并段最大的记录小时，就生成了一个初始归并段。用同样的方法继续生成下一个初始归并段，直到全部记录都处理完毕为止。
通过置换-选择排序算法得到的$m$个初始归并段长度可能是不同的。不同的归并策略可能导致归并次数的不同，即意味着需要的$I$/$O$操作次数不同，因此需要找出一种归并次数最少的归并策略来减少$I$/$O$操作次数，以提高排序效率。这就引出下一个知识点——最佳归并树。
归并过程可以用一棵树来形象地描述，这棵树称为归并树，树中结点代表当前归并段长度。初始记录经过置换-选择排序之后，得到的是长度不等的初始归并段，归并策略不同，所得的归并树也不同，树的带权路径长度（带权路径长度与$I$/$O$次数的关系为∶$I$/$O$次数=带权路径长度×2）也不同。为了优化归并树的带权路径长度，可将之前讲过的赫夫曼树运用到这里来，对于$k$路归并算法，可以用构造$k$叉赫夫曼树的方法来构造最佳归并树。
外部排序的时间复杂度涉及很多方面，且分析较为复杂，一般考试不会让考生分析整个流程中与时间复杂度相关的每一个细节，因此只需注意以下几点即可∶
1）m 个初始归并段进行 k 路归并，归并的趟数为$\lceil \log _km \rceil $。
2）每一次归并，所有记录都要进行两次$I$/$O$操作。
3）置换-选择排序这一步中，所有记录都要进行两次$I$/$O$操作。
4）置换-选择排序中，选最值那一步的时间复杂度要根据考试要求的选择算法而定。
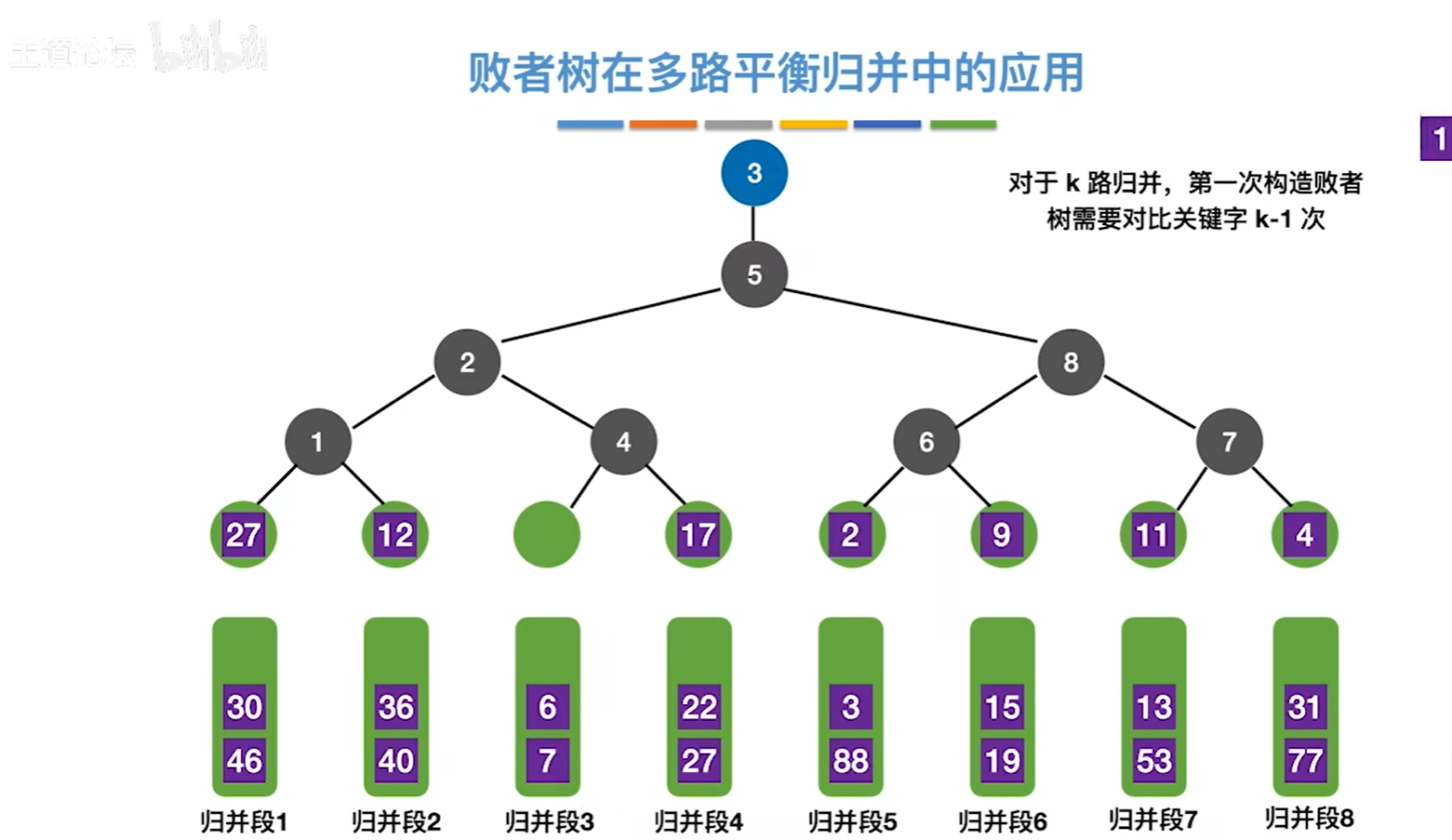
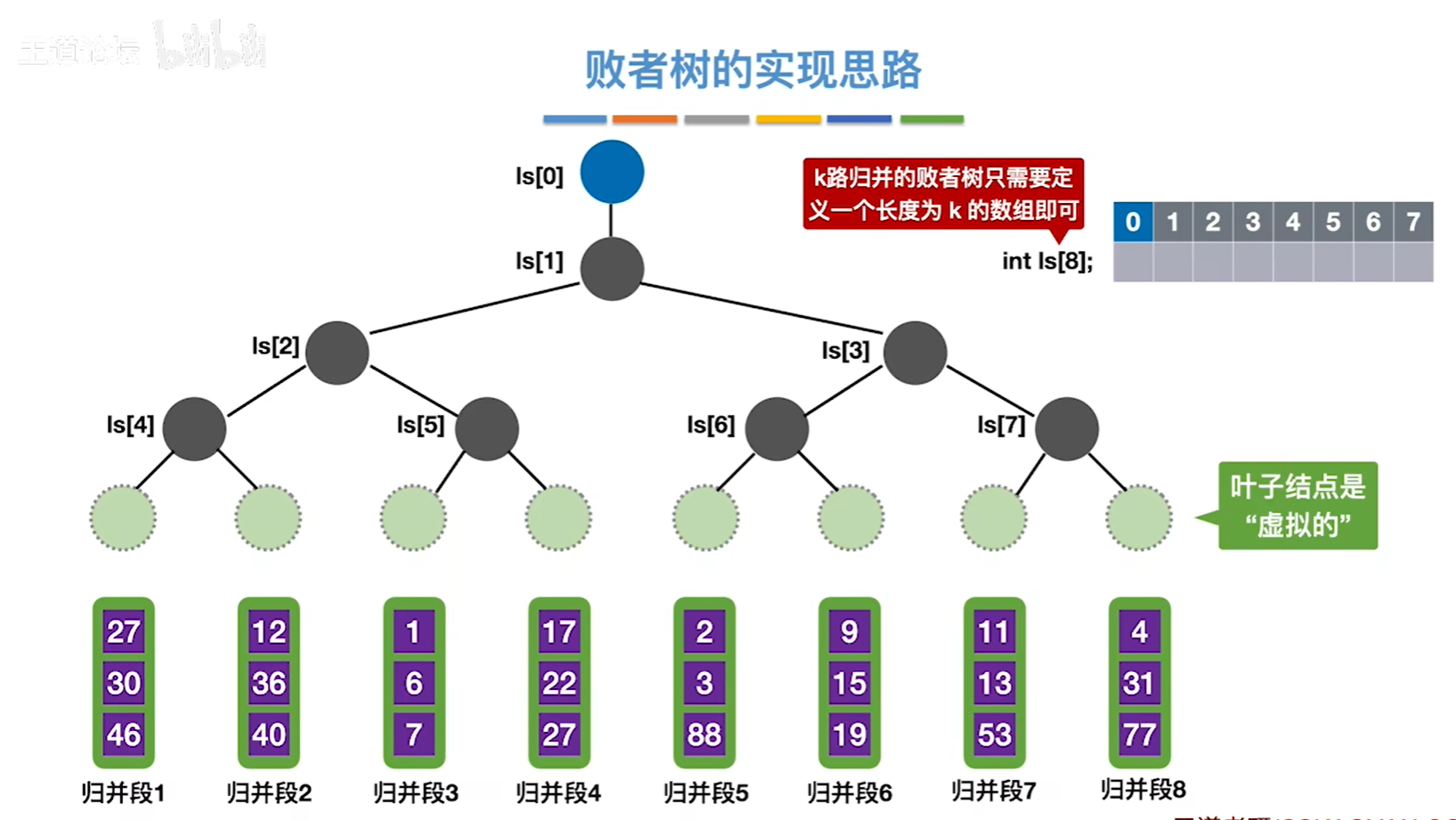
5）$k$路归并的败者树的高度为$\lceil \log _2k \rceil +1$，因此利用败者树从$k$个记录中选出最值需要进行$\lceil \log _2k \rceil $次比较，即时间复杂度是$O(\lceil \log _2k \rceil )$。
6）$k$路归并败者树的建树时间复杂度为$O(k\cdot log_2k)$。
所有步骤中的空间复杂度都是常量，因此是$O(1)$。
