若待排序表中有两个元素$R_i$和$R_j$,其对应的关键字相同即$key_i=key_j$,且在排序前$R_i$在$R_j$的前面,若使用某一排序算法排序后,$R_i$仍然在$R_j$的前面,则称这个排序算法是稳定的,否则称排序算法是不稳定的。算法是否具有稳定性并不能衡量一个算法的优劣,它主要是对算法的性质进行描述。如果待排序表中的关键字不允许重复,则排序结果是唯一的,那么选择排序算法时的稳定与否就无关紧要。
在排序过程中,根据数据元素是否完全在内存中,可将排序算法分为两类:
1、内部排序,是指在排序期间元素全部存放在内存中的排序;
2、外部排序,是指在排序期间元素无法全部同时存放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序。
一般情况下,内部排序算法在执行过程中都要进行两种操作:比较和移动。通过比较两个关键字的大小,确定对应元素的前后关系,然后通过移动元素以达到有序。当然,并非所有的内部排序算法都要基于比较操作,如基数排序就不基于比较。
每种排序算法都有各自的优缺点,适合在不同的环境下使用,就其全面性能而言,很难提出一种被认为是最好的算法。
插入排序
直接插入排序算法适用于顺序存储和链式存储的线性表。
//直接插入排序
void InsertSort(int A[], int n){
int i, j, temp;
for(i = 1; i < n; i++){
temp = A[i];
j = i - 1;
while(j >= 0 && temp < A[j]){
A[j + 1] = A[j];
j--;
}
A[j + 1] = temp;
}
}
直接插入排序算法中,每趟插入的过程中都进行了两项工作:1、从前面的有序子表中查找出待插入元素应该被插入的位置;2、给插入位置腾出空间,将待插入元素复制到表中的插入位置。在直接插入排序算法中,总是边比较边移动元素。下面将比较和移动操作分离,即先折半查找出元素的待插入位置,然后统一地移动待插入位置之后的所有元素。当排序表为顺序表时,可以对直接插入排序算法做如下改进:由于是顺序存储的线性表,所以查找有序子表时可以用折半查找来实现。确定待插入位置后,就可统一地向后移动元素。
折半插入排序仅减少了比较元素的次数,约为$O(n\cdot log_2n)$,该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数$n$;而元素的移动次数并未改变,它依赖于待排序表的初始状态。因此,折半插入排序的时间复杂度仍为$O(n^2)$,但对于数据量不很大的排序表,折半插入排序往往能表现出很好的性能。折半插入排序是一种稳定的排序方法。
//希尔排序
void shellSort(int a[], int n){
int i, j, gap; // gap 为步长,每次减为原来的一半。
for (gap = n / 2; gap > 0; gap /= 2){
// 共 gap 个组,对每一组都执行直接插入排序
for (i = 0; i < gap; i++){
for (j = i + gap; j < n; j += gap){
// 如果 a[j] < a[j-gap],则寻找 a[j]位置,并将后面数据的位置都后移。
if (a[j] < a[j - gap]){
int tmp = a[j];
int k = j - gap;
while (k >= 0 && a[k] > tmp){
k -= gap;
}
a[k + gap] = tmp;
}
}
}
}
}
交换排序
冒泡排序的基本思想是:从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即$A[i-1]>A[i]$),则交换它们,直到序列比较完。这被称为第一趟冒泡,结果是将最小的元素交换到待排序列的第一个位置(或将最大的元素交换到待排序列的最后一个位置),关键字最小的元素如气泡一般逐渐往上“漂浮”直至“水面”(或关键字最大的元素如石头一般下沉至水底)。下一趟冒泡时,前一趟确定的最小元素不再参与比较,每趟冒泡的结果是把序列中的最小元素(或最大元素)放到了序列的最终位置……这样最多做$n-1$趟冒泡就能把所有元素排好序。
//冒泡排序
void BubbleSort(int A[],int n){
for(int i = 0; i < n - 1; i++){
bool flag = false;
for(int j = n - 1; j > i; j--){
if(A[j - 1] > A[j]){
swap(A[j - 1],A[j]);
flag = true;
}
}
if(flag == false){
return;
}
}
}
//快速排序
void quick_sort(vector<int>& nums, int l, int r){
if (l >= r){
return;
}
int i = l - 1,j = r + 1, x = nums[i + j >> 1];
while(i < j){
do{
i++;
}while(nums[i] < x);
do{
j--;
}while(nums[j] > x);
if(i < j){
swap(nums[i], nums[j]);
}
}
quick_sort(nums, l, j),quick_sort(nums, j + 1, r);
}
选择排序
//选择排序
void SelectSort(int A[],int n){
for(i = 0; i < n - 1; i++){
min = i;
for(j = i + 1; j < n; j++){
if(A[j] < A[min]){
min = j;
}
}
if(min != i){
swap(A[i], A[min]);
}
}
}
void DownAdjust(int low, vector<int>& heap){
// low 为代调整节点
int i = low, j = i * 2;
while(j <= heap.size()){
if(j + 1 <= heap.size() && heap[j + 1] > heap[j]){
j = j + 1;
}
if(heap[j] > heap[i]){
swap(heap[j], heap[i]);
i = j;
j = i * 2;
}else{
break;
}
}
}
void CreateHeap(vector<int>& heap){
for(int i = n / 2; i >= 1; i--){
DownAdjust(i, heap);
}
}
归并排序
数组自顶向下版:
//归并排序
void merge_sort(int q[], int tmp[], int l, int r){
if(l >= r){
return;
}
int mid = l + r >> 1
merge_sort(q, tmp, l, mid);
merge_sort(q, tmp, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while(i <= mid && j <= r){
if(q[i] <= q[j]){
tmp[k++] = q[i++];
}else{
tmp[k++] = q[j++];
}
}
while(i <= mid){
tmp[k++] = q[i++];
}
while(j <= r){
tmp[k++] = q[j++];
}
for(i = l, j = 0; i <= r; i++, j++){
q[i] = tmp[j];
}
}
链表自顶向下版:
class Solution {
public:
//找到中间节点:two pointers
ListNode* find(ListNode* head){
ListNode* slow = new ListNode(0, head);
ListNode* fast = slow;
while(fast != nullptr && fast -> next != nullptr){
slow = slow -> next;
fast = fast -> next -> next;
}
return slow;
}
//合并子链表
ListNode* merge(ListNode* head1, ListNode* head2){
ListNode* pre = new ListNode();
ListNode* ret = pre;
while(head1 != nullptr && head2 != nullptr){
if(head1 -> val <= head2 -> val){
pre -> next = head1;
head1 = head1 -> next;
}else{
pre -> next = head2;
head2 = head2 -> next;
}
pre = pre -> next;
}
pre -> next = head1 != nullptr ? head1 : head2;
return ret -> next;
}
//递归调用自顶向下
ListNode* sortList(ListNode* head) {
if(head == nullptr){
return nullptr;
}
if(head -> next == nullptr){
return head;
}
ListNode* mid = find(head);
ListNode* head2 = mid -> next;
mid -> next = nullptr;
return merge(sortList(head), sortList(head2));
}
};
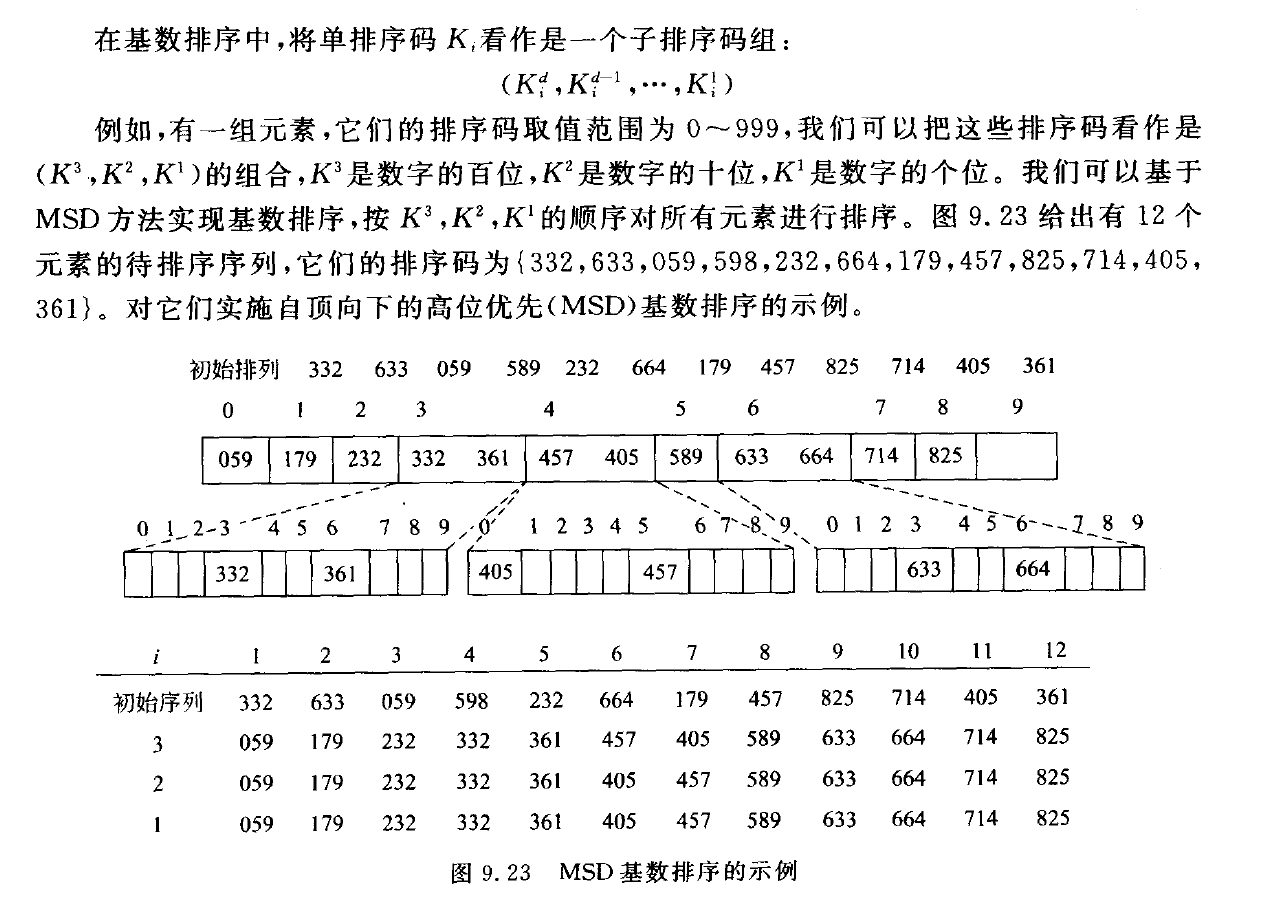
基数排序
内部排序总结
对排序算法的比较和应用应考虑以下情况:
1、选取排序方法需要考虑的因素:
①待排序的元素数目$n$。
②元素本身信息量的大小。
③关键字的结构及其分布情况。
④稳定性的要求。
⑤语言工具的条件,存储结构及辅助空间的大小等。
2、排序算法小结:
①若$n$较小,可采用直接插入排序或简单选择排序。由于直接插入排序所需的记录移动次数较简单选择排序的多,因而当记录本身信息量较大时,用简单选择排序较好。
②若文件的初始状态已按关键字基本有序,则选用直接插入或冒泡排序为宜。
③若$n$较大,则应采用时间复杂度为$O(nlogn)$的排序方法:快速排序、堆排序或归并排序。快速排序被认为是目前基于比较的内部排序方法中最好的方法,当待排序的关键字随机分布时,快速排序的平均时间最短。堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况,这两种排序都是不稳定的。若要求排序稳定且时间复杂度为$O(nlogn)$,则可选用归并排序。
④在基于比较的排序方法中,每次比较两个关键字的大小之后,仅出现两种可能的转移,因此可以用一棵二叉树来描述比较判定过程,由此可以证明:当文件的$n$个关键字随机分布时,任何借助于“比较”的排序算法,都至少需要$O(nlogn)$的时间。
⑤若$n$很大,记录的关键字位数较少且可以分解时,采用基数排序较好。
⑥当记录本身信息量较大时,为避免耗费大量时间移动记录,可用链表作为存储结构,此时仅修改相关结点的指针即可。