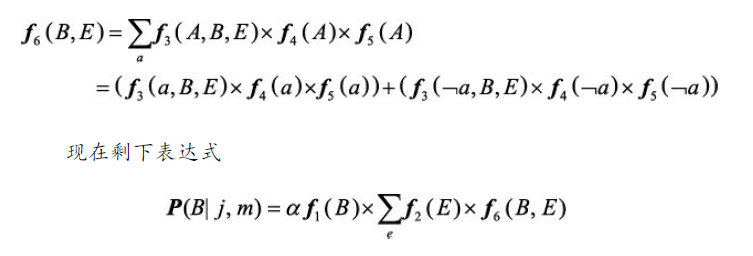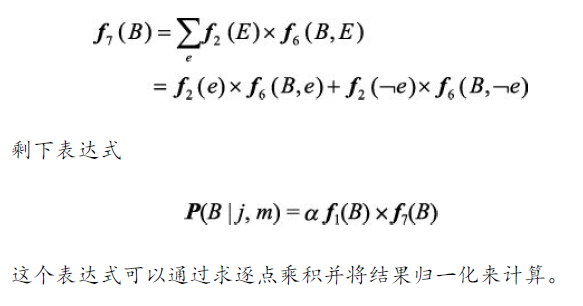引入
任何概率推理系统的基本任务都是给定一些观测到的事件——通常是一组证据变量的赋值,计算一组查询变量的后验概率分布。为了简化表示,每次只考虑一个查询变量;很多方法可以很容易地扩展到具有多个变量的查询。沿用之前的记号有:$X$表示查询变量;$E$表示证据变量$E_1,…,E_m$的集合,$e$是一个特定的观测事件;$Y$代表隐(非证据、非查询)变量$Y_1,…,Y_{\ell}$;因此$\left\{ X \right\} \cup E\cup Y$是全部变量集合,一个典型的查询为$P\left( X|e \right) $。接下来讨论用于计算后验概率的精确算法及其复杂性,事实证明,一般情况是难以处理的。
任何条件概率都可以通过对完全联合分布的项求和来计算。更具体地说,利用下式可以求解查询:
$$
P\left( X|e \right) =\alpha P\left( X,e \right) =\alpha \sum_y{P\left( X,e,y \right)}
$$
贝叶斯网络已经给出了完全联合分布的一个完整表示。更具体地说,下式表明联合分布中的项$P\left( X,e,y \right)$可以写作网络中条件概率的乘积。因此,可以通过计算贝叶斯网络中条件概率的乘积之和回答查询。
$$
P\left( x_1,…,x_n \right) =\prod_{i=1}^n{P\left( x_i|parent\left( X_i \right) \right)}
$$
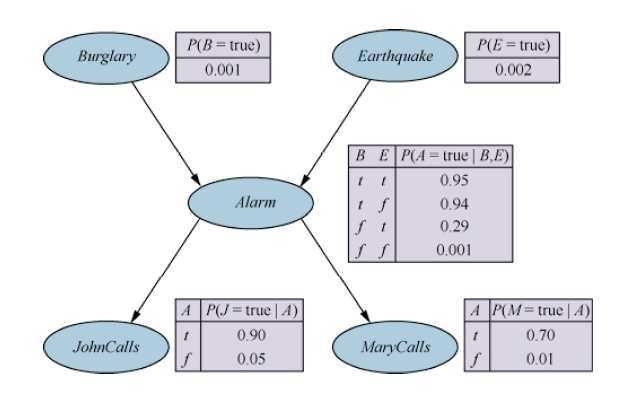
考虑如下贝叶斯网络上的查询$P\left( b|j,m \right) $:
根据完全联合分布可以得到:
$$
P\left( B|j,m \right) =\alpha P\left( B,j,m \right) =\alpha \sum_e{\sum_a{P\left( B,j,m,e,a \right)}}
$$
接下来以$B=true$为例,应用贝叶斯网络中条件概率的乘积之和得到:
$$
P\left( b|j,m \right) =\alpha \sum_e{\sum_a{P\left( b \right) P\left( e \right) P\left( a|b,e \right) P\left( j|a \right) P\left( m|a \right)}}
$$
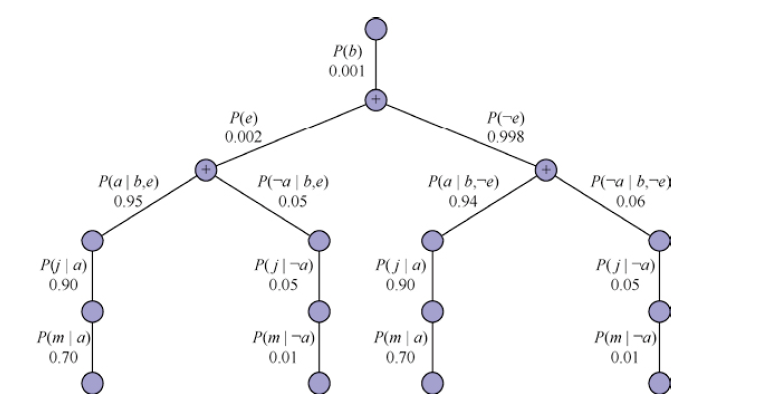
要计算这个表达式,必须对 4 项进行求和,每一项都是通过 5 个数相乘计算得到。在最坏的情况下,需要对几乎所有的变量求和,那么求和式中将有$O(2^n)$项,每一项都是$O(n)$个概率值的乘积。因此,直接实现的复杂性是$O(n\cdot 2^n)$。
利用计算的嵌套结构,可以将其复杂性简化为$O(2^n)$。这意味着对于类似前面的表达式,要尽可能地将求和向内移动。这样做是合法的,因为不是所有的概率乘积的因子都取决于所有的变量。因此可以得到:
$$
P\left( b|j,m \right) =\alpha P\left( b \right) \sum_e{P\left( e \right) \sum_a{P\left( a|b,e \right) P\left( j|a \right) P\left( m|a \right)}}
$$
这个表达式可以通过依次循环遍历变量,并在循环时乘以条件概率表表项来计算。对于每个求和,还需要对变量的可能的值进行循环。实际的求解算法使用深度优先、从左到右的递归方法计算表达式树。该算法在结构上与求解$CSP$的回溯算法和可满足性的$DPLL$算法非常相似。它的空间复杂性对于变量的数量只是线性的:算法在甚至没有明确构造完全联合分布的情况下对它求和。遗憾的是,对于含有$n$个布尔变量(不计数证据变量)的网络,它的时间复杂性总是$O(2^n)$——优于前面描述的简单方法的$O(n\cdot 2^n)$,但仍然相当可怕。
变量消元算法
通过观察表达式树可以发现其中出现了许多重复计算,通过消除这种重复计算,枚举算法可以得到极大的改进。其中的想法很简单:在计算一次之后保存结果供后续使用(通常是矩阵)。这是动态规划(或者记忆化搜索)的一种形式。该方法有若干种版本,这里介绍其中最简单的变量消元算法。变量消元通过从右到左的顺序计算表达式,在计算过程中存储中间结果,对每个变量的求和只计算依赖该变量的部分。
据此,用对应的因子的名称标记表达式的每个部分;每个因子是一个由其参数变量的值为索引的矩阵,对于证据变量因为其已被固定,不依赖其本身只依赖父节点,所以在因子中省略。故可将原式化为:
$$
P\left( B|j,m \right) =\alpha f_1\left( B \right) \times \sum_e{f_2\left( E \right) \times \sum_a{f_3\left( A,B,E \right) \times f_4\left( A \right) \times f_5\left( A \right)}}
$$
这里$\times $算子不是普通的矩阵乘积,而是逐点乘积算子,将在后面详细说明。计算过程根据各因子的逐点乘积(从右到左)对变量求和消元得到新因子,最后生成包含解的因子,也就是查询变量的后验分布。步骤如下:
首先,在$f_3\left( A,B,E \right) $、$f_4\left( A \right) $和$f_5\left( A \right)$中求和消元$A$得到新的因子$f_6\left( B,E \right) $,以$B,E$作为索引:
然后,从$f_2\left( E \right) $和$f_6\left( B,E \right) $的乘积中求和消元 E:
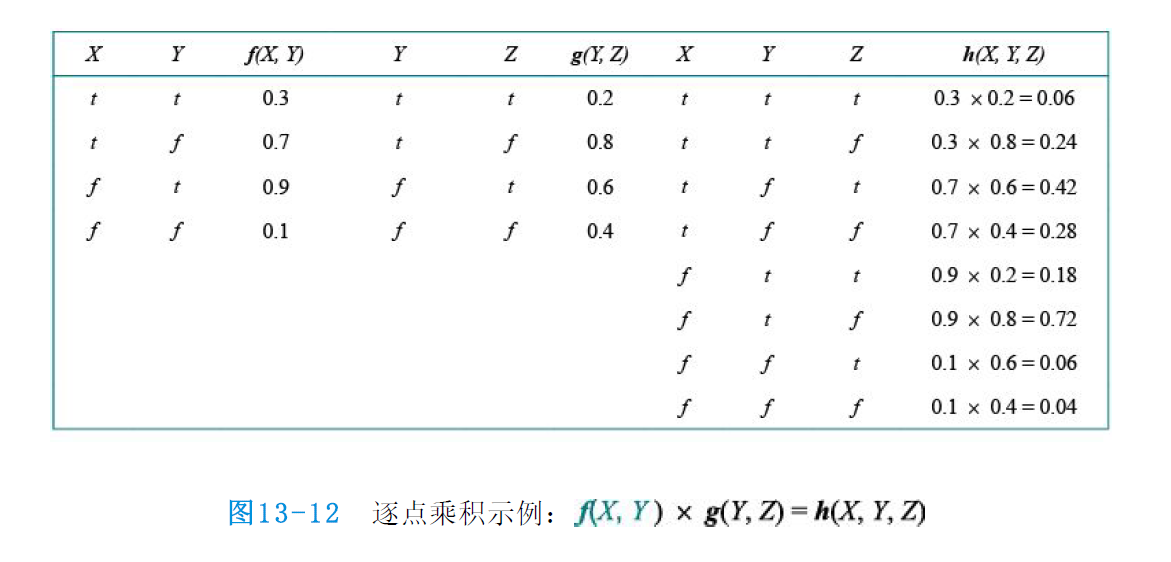
检查这个计算过程,可以看到需要两个基本的计算操作:求两个因子的逐点乘积,以及从因子的乘积中求和消元一个变量。
两个因子$f$与$g$的逐点乘积生成了一个新因子$h$,它的变量是$f$与$g$中变量的并集,元素由这两个因子中相应元素的乘积给出。由逐点相乘得到的因子可以包含比任何被乘的因子更多的变量,并且因子的规模与变量的数量呈指数关系。这就是变量消元算法中空间复杂性和时间复杂性所在。
从因子的乘积中求和消元一个变量是通过依次固定该变量的每个值得到的子矩阵相加来完成的。例如,为了从$h(X, Y, Z)$中求和消元$X$:
唯一需要注意的技巧是——任何不依赖于待求和消元的变量的因子都可以移到求和符号之外。这可能比先计算更大的逐点乘积$h$再从中求和消元$X$更高效。注意,直到需要从累加的乘积中对一个变量求和消元时,才进行矩阵相乘。那时只需要将那些包含待求和消元的变量的矩阵相乘。给定逐点乘积和求和消元函数,变量消元算法本身可以写得非常简单:
如前面伪码描述的算法中包含一个未描述的$Order$函数来为变量选择排序。每一种排序选择都会生成一个有效的算法,但不同的排序会导致在计算过程中产生不同的中间因子。
一般,变量消元的时间和空间要求是由算法运行过程中构造的最大因子的规模决定的,这又由变量的消元顺序和网络的结构决定。事实证明,确定最优排序是难以求解的问题,但有一些好的启发式方法。一个相当有效的方法是贪心法:消除那些使下一个被构造的因子规模最小的变量。
此外,值得注意的是可能存在一些变量与查询无关。一般,可以删除任何非查询变量或非证据变量的叶节点。在删除了它们之后,可能会发现更多无关的叶节点。如果反复进行这一过程,最终可以发现,每个不是查询变量或证据变量祖先节点的变量都与查询无关。因此,变量消元算法可以在评估查询之前删除所有这类变量。
进一步深入
贝叶斯网络中精确推断的复杂性高度依赖于网络的结构。入室盗窃网络代表了一簇网络,在这族网络中,任意两个节点之间最多只有一条无向路径(即忽略箭头的方向)。这族网络叫作单连通网络或者多重树,它们有一个特别好的性质:多重树中精确推断的时间复杂性和空间复杂性与网络规模呈线性关系。这里所说的规模定义为条件概率表表项的数量;如果每个节点的父节点数量由一个常数限制,那么复杂性也与节点数量呈线性关系。这些结果适用于与网络拓扑排序一致的任何排序。
对于多连通网络,即使每个节点的父节点数量有界,在最坏情况下,变量消元仍然有着指数量级的时间复杂性和空间复杂性。如果考虑到因为它包括命题逻辑推断作为特例,所以贝叶斯网络中的推理是$NP$困难的。此外,可以进一步证明贝叶斯网络推断是$\# P$困难的,严格地难于$NP$完全问题。
贝叶斯网络推断的复杂性与约束满足问题的复杂性之间有着密切的联系。求解离散$CSP$的难度与约束图的“树状”程度有关。诸如树宽这样的限制求解$CSP$复杂性的度量,也可以直接应用于贝叶斯网络之中。此外,变量消元算法可以像在贝叶斯网络上一样推广到求解$CSP$。
除了将可满足性问题归约到贝叶斯网络推断,还可以将贝叶斯网络推断归约到可满足性,这样可以利用为$SAT$求解而发展出的强大机制。在这种情况下,将推断问题归约为$SAT$求解的一种特殊形式,称之为加权模型计数($WMC$)。常规模型计数会计算$SAT$表达式可满足的赋值数量; $WMC$将这些可满足赋值的总权重相加,在这个应用中,权重本质上是给定父变量时每个变量赋值的条件概率的乘积。某种程度上因为$SAT$求解技术已经针对大规模应用进行了优化,通过$WMC$进行的贝叶斯网络推理在大树宽网络上与其他精确算法相比是有竞争力的,有时甚至优于它们。
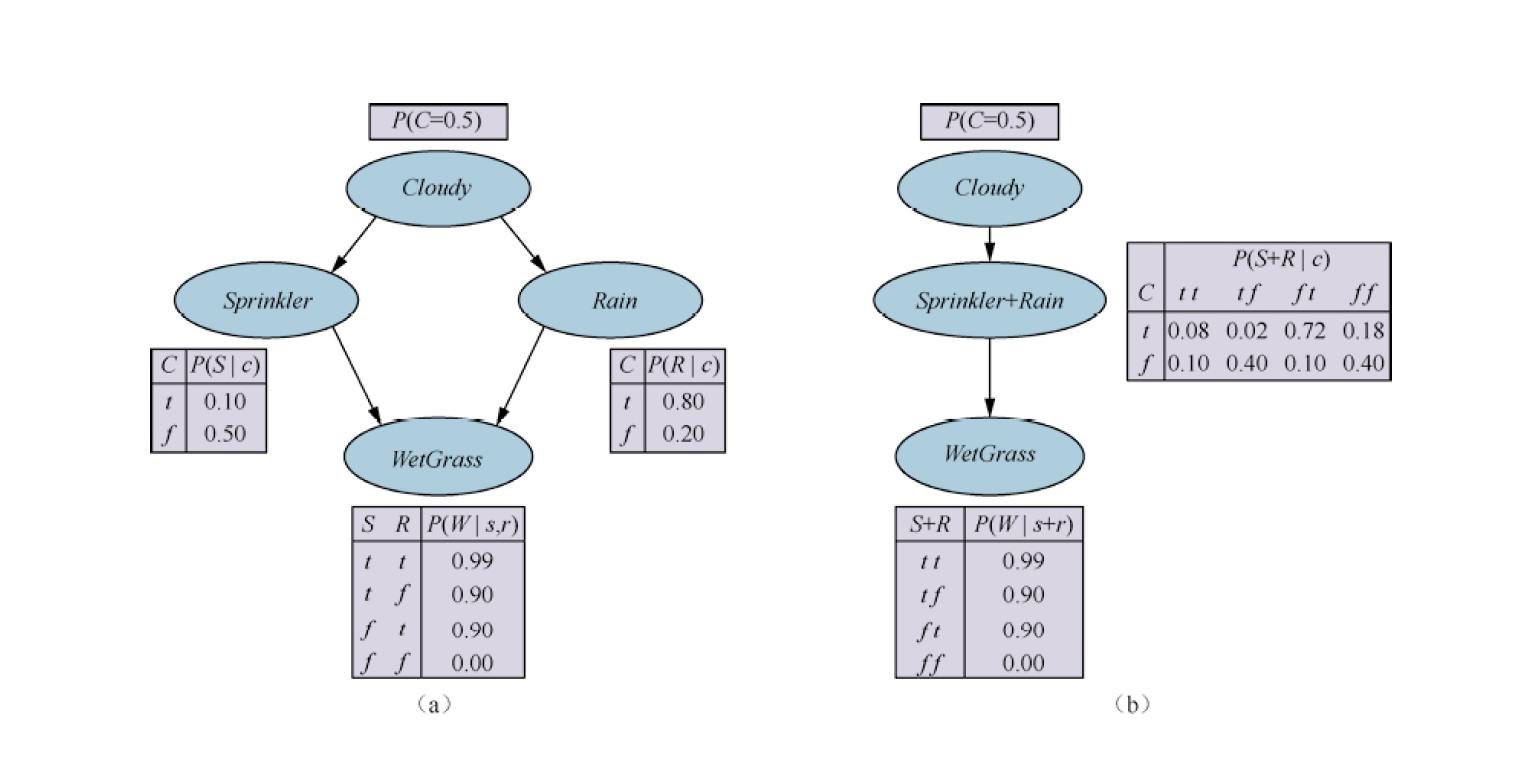
变量消元算法在回答单个查询时简单有效。但是,如果要计算网络中所有变量的后验概率,它的效率可能较低。例如,在多重树网络中可能需要处理$O(n)$个查询,每个耗时$O(n)$,那总共需要$O(n^2)$时间。使用聚类算法[也叫作连接树算法]可以把时间减少到$O(n)$。因此,这些算法在贝叶斯网络相关的商业工具中得到了广泛应用。
聚类的基本思想是将网络中的单个节点连接起来,形成簇节点,使得最终得到的网络是多重树,同时聚类的过程通常会产生共享一些变量的大节点。
一旦网络转换为多重树形式,就需要一种特殊的推断算法,因为传统的推断方法无法处理彼此共享变量的大节点。从本质上讲,该算法是约束传播的一种形式,其中约束确保相邻的大节点在它们共享的任何变量的后验概率上达成一致。通过仔细记录,该算法能够在与聚类网络规模呈线性关系的时间内为网络中所有非证据节点计算后验概率。但是,问题的$NP$困难本质并未改变:如果一个网络的变量消元需要指数级的时间与空间,那么聚类网络中的条件概率表必然也会是指数级规模。