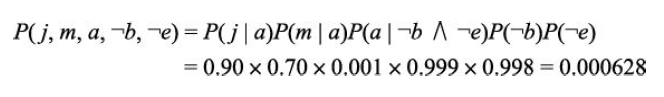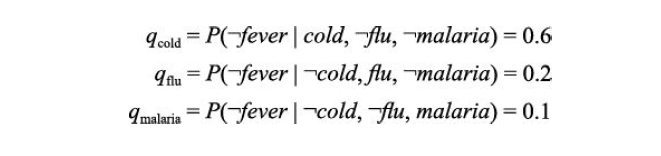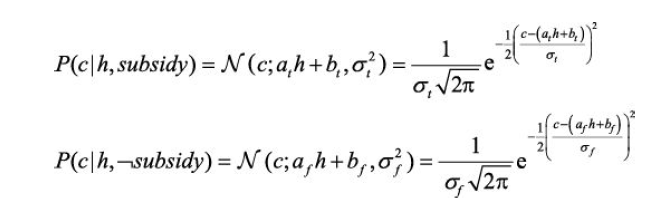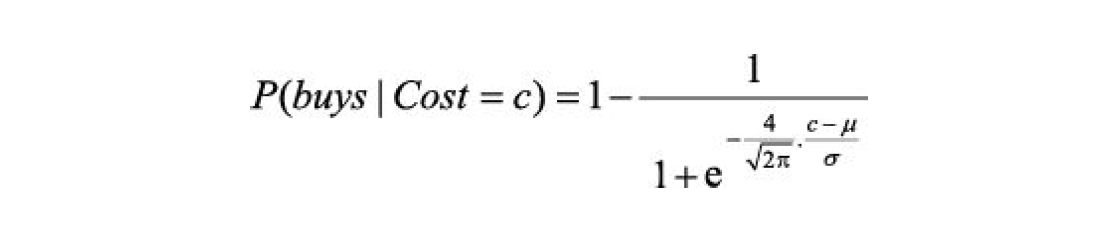引入
贝叶斯网络($Bayesian$ $network$)是一种数据结构,用于表示变量之间的依赖关系。贝叶斯网络可以本质上表示任何完全联合概率分布,并且它在很多情况下可以非常简洁。
贝叶斯网络是一个有向图,其中每个节点用定量的概率信息标记,完整的描述如下:
(1)每个节点对应一个随机变量,它可以是离散的,也可以是连续的。
(2)有向链路或箭头连接成对的节点。如果有从节点$X$指向节点$Y$的箭头,则称$X$是$Y$的一个父节点。图中没有有向环,因此它是一个有向无环图(简称$DAG$)。
(3)每个节点$X_i$关联概率信息$\theta \left( X_i|Parent\left( X_i \right) \right) $,使用有限的参数量化父节点对该节点的影响。
网络的拓扑以精确简洁的方式指定了在域中成立的条件独立性关系。箭头的直观含义通常是$X$对$Y$有直接影响,这意味着原因通常是结果的父节点。这种方式比实际指定概率本身要容易得多,一旦确定了贝叶斯网络的拓扑结构,就只需要以给定其父节点的条件分布的形式来指定每个变量的局部概率信息。所有变量的完全联合分布由拓扑结构和局部概率信息定义。
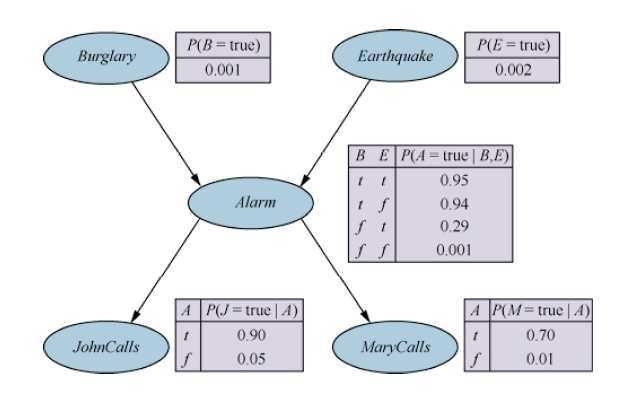
贝叶斯网络的语法由一个每个节点都附加一些局部概率信息的有向无环图组成。语义定义了语法如何对应于网络的变量的联合分布。每个节点的局部概率信息采用条件概率表的形式表示(离散变量)。条件概率表的每一行包含某个条件事件下每个节点的值的条件概率。对于没有父节点的节点,其条件概率表只有一行,表示变量每个可能的值的先验概率。
假设贝叶斯网络包含$n$个变量$X_1, …, X_n$。那么联合分布的一个通用条目是$P\left( X_1=x_1\land …\land X_n=x_n \right) $,或者缩写成$P(x_1, …, x_n)$。贝叶斯网络的语义将联合分布中的每个条目定义如下:
$$
P\left( x_1,…,x_n \right) =\prod_{i=1}^n{\theta \left( x_i|Parent\left( X_i \right) \right)}
$$
以上表明,任意联合分布中的每一项都由贝叶斯网络中局部条件分布的适当元素的乘积来表示。如在前面图片所示的贝叶斯网络下有:
此外,局部条件分布可以从联合分布中计算得到:
$$
\theta \left( x_i|Parent\left( X_i \right) \right) \equiv P\left( x_i|Parent\left( X_i \right) \right) \equiv \frac{P\left( x_i,Parent\left( X_i \right) \right)}{P\left( Parent\left( X_i \right) \right)}
$$
$$
=\frac{\sum_y{P\left( x_i,Parent\left( X_i \right) ,y \right)}}{\sum_{x’,y}{P\left( x_{i}^{‘},Parent\left( X_i \right) ,y \right)}}
$$
这意味着在估计局部条件分布的值时,它们应当是给定父节点时该变量的真实条件概率。网络的每一个参数都只在一个变量的小集合上具有明确的含义,这一事实对于模型的健壮性和易描述性至关重要。
对贝叶斯网络联合分布的通用条目应用乘法法则可以得到:
$$
P\left( x_1,…,x_n \right) =P\left( x_n|x_{n-1},…,x_1 \right) P\left( x_{n-1},…,x_1 \right)
$$
$$
=P\left( x_n|x_{n-1},…,x_1 \right) P\left( x_{n-1}|x_{n-2},…,x_1 \right) \cdot \cdot \cdot P\left( x_2|x_1 \right) P\left( x_1 \right)
$$
$$
=\prod_{i=1}^n{P\left( x_i|x_{i-1},…,x_1 \right)}
$$
上式被称为链式法则,它对任何随机变量集合都成立。将上式与通用条目相比较可以发现对于网络中的每个变量$X_i$,假设$Parent\left( X_i \right) \subseteq \left\{ X_{i-1},…X_1 \right\} $成立,则有:
$$
P\left( X_i|X_{i-1},…,X_1 \right) =P\left( X_i|Parent\left( X_i \right) \right)
$$
通过拓扑排序进行编号不难得到使$Parent\left( X_i \right) \subseteq \left\{ X_{i-1},…X_1 \right\} $成立的序列。同时也意味着只有在给定父节点,每个节点条件独立于节点排序中的其他前驱节点时,贝叶斯网络才是域的正确表示。据此,可以得到构建这一条件的贝叶斯网络方法:
(1)节点:首先确定建模域所需的变量集合,再对它们进行排序,得到$\left\{ X_1,…,X_n \right\} $。任何排序的顺序都是可行的,但是如果变量的顺序是原因先于结果的,那么产生的网络会更紧凑。
(2)链路:i 从 1 到 n,循环顺序执行以下操作:1、从$\left\{ X_1,…,X_{i-1} \right\} $中为节点$X_i$选择最小父节点集合,使得$P\left( X_i|X_{i-1},…,X_1 \right) =P\left( X_i|Parent\left( X_i \right) \right) $成立;2、为每个父节点插入一条从父节点到$X_i$的链路;3、记录条件概率表$P\left( X_i|Parent\left( X_i \right) \right) $。
由于每个节点只与前面的节点相连,这种构建方法保证了网络是无环的。贝叶斯网络的另一个重要性质是它不包含冗余的概率值。如果没有冗余,就不可能产生不一致的网络:知识工程师或领域专家不可能创建一个违反概率公理的贝叶斯网络。
贝叶斯网络除了可以作为域的完整且非冗余的表示,通常还比完全联合分布更紧凑。这个性质使得处理具有许多变量的域成为可能。贝叶斯网络的紧凑性是局部结构化系统一般性质的一个示例。在局部结构化的系统中,每个子组件仅与有限数量的其他组件直接交互,而与组件总数无关。局部结构化在复杂度上的增长速度通常是线性的而非指数级别的。
在使用贝叶斯网络时,在大多数域中可以合理地假设:每个随机变量最多受到$k$个其他随机变量的直接影响,其中$k$是某个常数。此时贝叶斯网络的规模是相当大的,通常的做法是在变量之间的依赖关系微弱时忽略该链路,因为通过增加网络额外的复杂性以获得精度上的一点点提高并不值得。实践中,对于某个链路是否加入取决于指定额外信息的代价与得到更准确概率的重要性之间的权衡。
即使在局部结构化的域内,也只能在节点顺序选择合适的情况下得到一个紧凑的贝叶斯网络。如果选择了错误的节点顺序首先会导致链路增多且一些链路表示的关系十分脆弱,对它们的概率判断困难且不自然。此外也会导致无法表明所有的条件独立性关系,因此最终指定了许多不必要的数值。
贝叶斯网络的语义
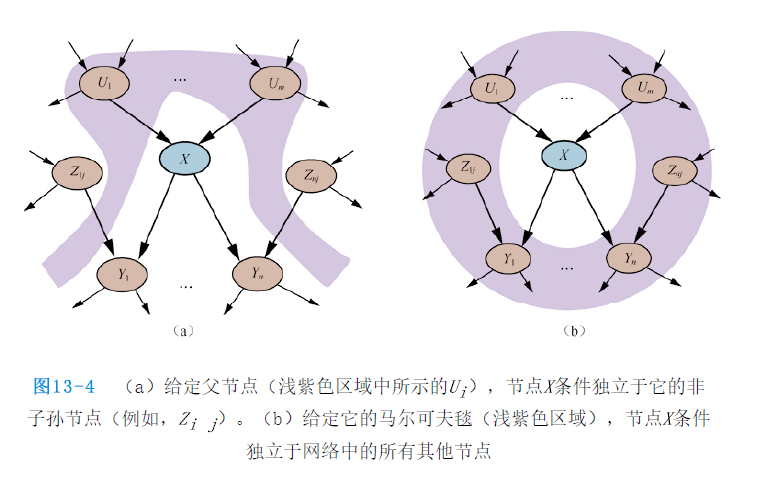
由前面可以明白给定父节点,一个变量条件独立于它的其他前驱变量。当然也可以证明更一般的“非子孙”性质:给定父节点,每个变量条件独立于它的非子孙节点。换句话说,可以用另一种方式来看待贝叶斯网络的语义:网络定义了一个条件独立性性质的集合,而不是将完全联合分布定义为条件分布的乘积。完全联合分布也可以由这些性质推导得出。
另一个重要的独立性性质蕴含在非子孙性质中:给定一个变量的父节点、子节点和子节点的父节点,即给定它的马尔可夫毯,其条件独立于网络中所有其他节点。马尔可夫毯的性质使得使用完全局部随机采样过程和分布式随机采样过程的推断算法成为可能。
在处理贝叶斯网络时,人们通常会对条件独立性有这样的问题:给定第三个集合$Z$,节点集合$X$是否条件独立于另一个集合$Y$。这个问题可以通过检查贝叶斯网络的集合$Z$是否$d$分离集合$X$和$Y$来高效地确定。其具体过程如下:
(1)只考虑包含$X$、$Y$、$Z$和它们祖先的祖先子图。
(2)在任何无链路相连的共享公共子节点的节点对之间添加链路;得到所谓的道德图。
(3)用无向链路替换所有有向链路。
(4)在得到的图中,如果$Z$阻塞了所有$X$和$Y$之间的路径,则$Z$ $d$分离$X$和$Y$。那样的话,给定$Z$时,$X$将条件独立于$Y$。否则,原始贝叶斯网络不要求条件独立性。
简而言之,$d$分离意味着在无向的、道德的、祖先子图中分离。注意,马尔可夫毯性质直接遵循$d$分离性质,因为一个变量的马尔可夫毯将它与其他所有变量$d$分离。
即使最大父节点的数量$k$很小,为一个节点填充条件概率表也需要$O(2^k)$个数值,并且可能需要对所有可能的条件事件有大量的经验。事实上,这是最坏的情况,父节点和子节点之间的关系是完全任意的。通常,这种关系可以通过符合某种标准模式的正则分布来描述。在这种情况下可以通过命名使用的模式并提供一些参数来指定完整的表。
最简单的例子是确定性节点。确定性节点的值完全由其父节点的值指定,没有任何不确定性。这种关系可以是逻辑关系,也可以是数值关系。许多贝叶斯网络系统允许用户使用通用编程语言来指定确定性函数;这使得在概率模型中包含诸如全球气候模型或电网模拟器等复杂元素成为可能。
另一个在实践中经常出现的重要模式是特定于上下文的独立性($CSI$)。如果给定其他变量的某些值,一个变量条件独立于它的一些父节点,则这个条件分布存在$CSI$。贝叶斯网络系统通常使用$if$-$then$-$else$语法来指定条件分布以实现$CSI$,例如:
其中$d_1$和$d_2$表示任意的分布。与确定性的情况一样,网络中存在的$CSI$有利于高效的推断。
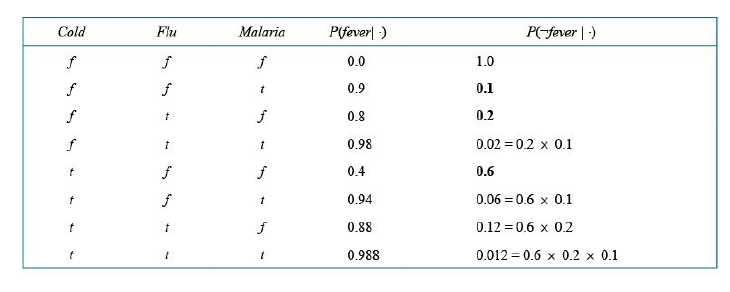
不确定关系通常可以利用所谓的噪声逻辑关系来刻画。其中一个典型的例子是噪声或关系,它是逻辑或的推广。噪声或模型为每个父节点导致子节点为真的能力引入了不确定性,父节点与子节点之间的因果关系可能会被抑制,因此病人可能感冒,但可能不发烧。
该模型做了两个假设。首先,假设所有可能的原因都被列出。[如果遗漏了一些原因,则总是增加一个所谓的遗漏节点来涵盖“其他原因”]。其次,它假设每个父节点受到的抑制独立于其他父节点受到的抑制,例如,无论什么原因抑制了$Malaria$引起发烧,它都独立于其他的抑制$Flu$引起发烧的原因。在这两个假设下,$Fever$为假当且仅当它所有为真的父节点都被抑制,这个概率是它的每个父节点被抑制的概率$q_j$的乘积。假设这些个体抑制概率如下:
根据这些信息和噪声或假设,可以构建完整的条件概率表:
$$
P\left( x_i|parent\left( X_i \right) \right) =1-\prod_{\left\{ j;X_j=true \right\}}{q_j}
$$
其中的乘积是条件概率表中那一行中值为真的父节点的乘积:
通常,一个依赖于$k$个父节点的变量的噪声逻辑关系可以用$O(k)$个参数而非$O(2^k)$来描述完全条件概率表,这使得评估和学习更加容易。
许多真实世界的问题涉及连续值,例如高度、质量、温度和金钱。根据定义,连续变量有无限多个可能的值,因此明确地为每个值指定条件概率是不可能的。处理连续变量的一种方法是离散化,在选择类别数量时,需要在准确率损失和可能导致运行时间慢的庞大条件概率表之间进行权衡。
另一种方法是使用一族标准的概率密度函数来定义连续变量。例如,指定高斯(或正态)分布$\mathscr{N}\left( x;\mu ,\sigma ^2 \right) $只需要两个参数,即均值$\mu $和方差$\sigma ^2$。还可以使用一种被称为非参数表示的解决方法,用一组实例隐式地定义条件分布,其中每个实例都包含父变量和子变量的特定值。
同时具有离散变量和连续变量的网络称为混合贝叶斯网络。要指定混合网络,就必须指定两种新的分布:给定离散或连续父节点的连续变量的条件分布;以及给定连续父节点的离散变量的条件分布。
首先关注子节点为连续值的情况,对于离散的父节点,将通过枚举的方式处理。而为了处理连续的父节点,将指定子节点的分布如何依赖于父节点的连续值$h$。换句话说,将价格分布的参数指定为$h$的函数。最常见的选择是线性高斯条件分布,其中子节点具有高斯分布,且均值$\mu $随着父节点的值线性变化,标准差$\sigma $固定。如:
线性高斯条件分布具有一些特殊的性质。只包含线性高斯分布的连续变量的网络在所有变量上的联合分布也是多元高斯分布。并且变量在给定任何证据后的后验分布也具有这个性质]。因此,当增加离散变量作为连续变量的父节点(不是子节点)时,网络定义了一个条件高斯分布:对离散变量给定任意值,连续变量的分布是多元高斯分布。
接下来转而考虑具有连续父节点的离散变量的分布,通过合理假设可以认为条件分布表现得像一个“软”阈值函数。一种构造软阈值的方式是使用标准正态分布的积分:
$$
\varPhi \left( x \right) =\int_{-\infty}^x{\mathcal{N}\left( s;0,1 \right) ds}
$$
可以从如下角度确认这种软阈值形式的合理性:潜在的决策过程具有某种硬阈值,但是该阈值的精确位置受到随机高斯噪声的影响。概率单位模型的另一种选择是使用$expit$或逆$logit$模型。它使用逻辑斯谛函数$1/\left( 1+e^{-x} \right) $生成软阈值——它将$x$的任意值映射到$0$与$1$之间:
前面两个软阈值函数在图像上看起来十分相似,但$logit$事实上“尾部”更长。概率单位通常更适合实际场景,但逻辑斯谛函数有时在数学上更容易处理,因此在机器学习中有着广泛的应用。这两种模型都可以通过父节点值的线性组合来处理多个连续父节点。这也适用于离散父节点的值是整数的情况。例如,对于$k$个布尔父节点,每个父节点都可以视为取值$0$或$1$,$expit$或概率单位分布的输入将是一个带有$k$个参数的加权线性组合,得到一个与前面讨论的噪声或模型非常相似的模型。
连续变量可以提供更高的精度,但是除了在一些特殊情况下,对连续变量的精确推断是不可能的。一个具有许多可能的值的离散变量会使得填写相应的巨大条件概率表变得单调乏味,并且使精确推断复杂性更高(除非该变量的值总是被观测到的)。