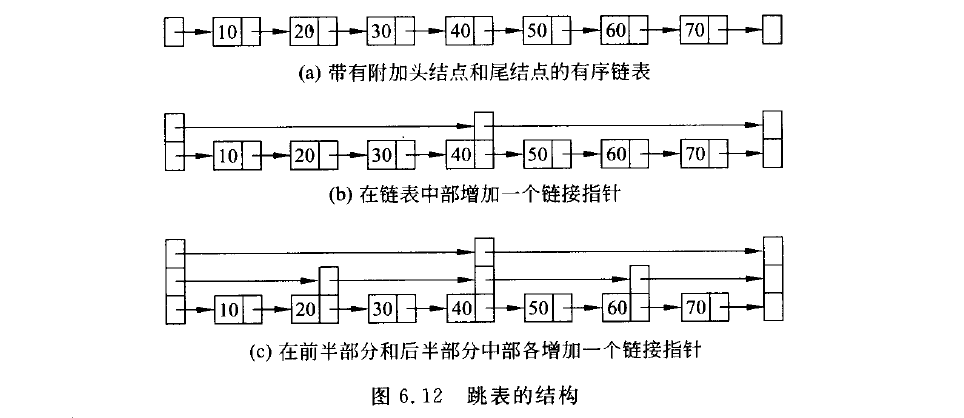
跳转表
每一水平列表称作一层($level$),其中$S_0$和$S_h$分别称作底层($bottom$)和顶层($top$)。与通常的列表一样,同层节点之间可定义前驱与后继关系。为便于查找,同层节点都按关键码排序。需再次强调的是,这里的次序只是内部的一种约定;对外部而言,各词条之间仍然只需支持判等操作即可。
层次不同的节点可能沿纵向组成塔,同一塔内的节点以高度为序也可定义前驱与后继关系。塔与词典中的词条一一对应。尽管塔内的节点相互重复,但正如随后将要看到的,这种重复不仅可以加速查找,而且只要策略得当,也不至造成空间的实质浪费。
跳表的查找思路类似二分查找,从顶层开始向下搜索;不难理解,其中各塔高度的随机分布规律(如最大值、平均值等),对跳转表的总体性能至关重要。反之,若不就此作出显式的限定,则跳转表的时间和空间效率都难以保证。在极端情况下,每个词条所对应塔的高度均有可能接近甚至达到$h$,同时,若词条总数为$n$,则在此类情况下,跳转表所需的存储空间量也将高达$O(nh)$。若能采用简明而精妙的策略,控制跳转表的生长过程,则在时间和空间方面都可实现足够高的效率。就效果而言,此类控制策略必须满足所谓“生长概率逐层减半”条件:
对于任意$0 \le k < h$,$S_k$中任一节点在$S_{k+1}$中依然出现的概率,始终为$1/2$。在此情况下的空间复杂度为$O(n)$,同时时间复杂度为$O(logn)$。跳表的插入过程为插入后从塔底开始生长,模拟投掷硬币,为正生长一层为反则停止生长。插入算法运行时间期望值的上界为$O(logn)$。删除操作则在各层删除即可,时间复杂度亦为$O(logn)$。
散列表
散列函数设计最为重要的一条原则就是,关键码映射到各桶的概率应尽量接近于$1/M。若关键码均匀且独立地随机分布,这也是任意一对关键码相互冲突的概率。就整体而言,这等效于将关键码空间“均匀地”映射到散列地址空间,从而避免导致极端低效的情况。总而言之,随机越强、规律性越弱的散列函数越好。当然,完全符合上述条件的散列函数并不存在,只能通过先验地消除可能导致关键码分布不均匀的因素,最大限度地模拟理想的随机函数,尽最大可能降低发生冲突的概率。
除余法是符合上述要求的一种最简单的映射办法,就是将散列表长度$M$取作为素数,并将关键码$key$映射至$key$关于$M$整除的余数。
MAD 法:以素数为表长的除余法尽管可在一定程度上保证词条的均匀分布,但从关键码空间到散列地址空间映射的角度看,依然残留有某种连续性。将关键码$key$映射至$(a*key+b) mod M$,此类散列函数需依次执行乘法、加法和除法(模余)运算,故此得名。尽管运算量略有增加,但只要常数 a 和 b 选取得当,MAD 法可以很好地克服除余法原有的连续性缺陷。
数字分析法从关键码$key$特定进制的展开中抽取出特定的若干位,构成一个整型地址。
平方取中法,从关键码$key$的平方的十进制或二进制展开中取居中的若干位,构成一个整型地址。
折叠法,是将关键码的十进制或二进制展开分割成等宽的若干段,取其总和作为散列地址。
位异或法,是将关键码的二进制展开分割成等宽的若干段,经异或运算得到散列地址。
(伪)随机数法:这一策略的原理也可理解为,将“设计好散列函数”的任务,转换为“设计好的(伪)随机数发生器”的任务。幸运的是,二者的优化目标几乎是一致的。需特别留意的是,由于不同计算环境所提供的(伪)随机数发生器不尽相同,故在将某一系统中生成的散列表移植到另一系统时,必须格外小心。
多槽位法:将彼此冲突的每一组词条组织为一个小规模的子词典,分别存放于它们共同对应的桶单元中。比如一种简便的方法是,统一将各桶细分为更小的称作槽位的若干单元,每一组槽位可组织为向量或列表。
独立链法:冲突排解的另一策略与多槽位法类似,也令相互冲突的每组词条构成小规模的子词典,只不过采用列表(而非向量)来实现各子词典。
公共溢出区法:在原散列表之外另设一个词典结构,一旦在插入词条时发生冲突就将该词条转存至另一词典结构中。就效果而言,另一词典结构相当于一个存放冲突词条的公共缓冲池,该方法也因此得名,此时的散列表也可理解为是一种递归形式的散列表。
线性试探法:开放定址策略最基本的一种形式是:在插入关键码$key$时,若发现桶单元已被占用,则转而试探桶单元+1;+1 也被占用,则继续试探+2;…;如此不断,直到发现一个可用空桶。当然,为确保桶地址的合法,最后还需统一对 M 取模。
平方探测法平方探测法所得到的序列为$d+1^2$、$d-1^2$、$d+2^2$、$d-2^2…$平方探测法是一种较好的处理冲突的方法,可以减少堆积问题的出现。它的缺点是不能探查到$Hash$中的所有单元,但至少能够探测一半。