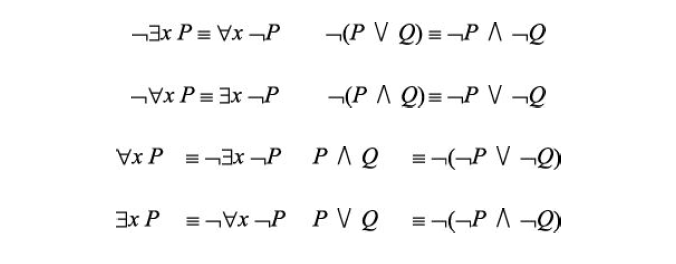一阶逻辑的语法和语义
一阶逻辑模型具有对象,模型的域是它包含的对象集或域元素的集合。域应当是非空的——每个可能世界至少要含有一个对象。数学上来说,对象是什么无所谓——有意义的只是每个特定模型中有多少对象。 模型中的对象可能有多方面的关系。从形式上来看,关系就是相关对象的元组集。(一个元组是以固定顺序排列的一系列对象,使用尖括号将对象括起来表示。)二元关系关联一对对象,一元关系通常称为属性。
最好将某些类型的关系视为函数,因为这样的话给定一个对象,它必然仅关联到一个对象。例如,每个人都有一条左腿,因此模型含有一个一元“左腿”函数,即从一个单元素元组到一个对象的映射。严格来说,一阶逻辑中的模型需要全函数,也就是对于所有输入的元组都要有值。这样,王冠必须要有一条左腿,每条左腿也一样。对于这种尴尬的问题有一个技术解决方案,它需要增加一个“不可见”的对象来作为一切没有左腿的东西的左腿,包括它自己。幸运的是,只要没人对没有左腿的东西的左腿进行断言,这些技术细节就不重要。
形式化文法的完整描述:
一阶逻辑的基本语法元素是代表对象、关系和函数的符号。因此,符号分为 3 种:代表对象的常量符号、代表
关系的谓词符号和代表函数的函数符号。与命题符号一样,如何命名完全取决于使用者的意愿。每个谓词和函数符号都有一个决定参数数量的元数。每个模型必须提供所需的信息来确定任意给定语句为真还是为假。因此,除了它的对象、关系和函数,每个模型还要包含一套确切指明常量、谓词和函数符号指代的是哪个对象、关系和函数的解释。当然,模型还有很多种可能的解释。
总之,一阶逻辑中的模型包含一个对象集和一种解释,这种解释将常量符号映射到对象、将函数符号映射到关于这些对象的函数,将谓词符号映射到关系。与命题逻辑一样,蕴含、有效性等都是用所有可能模型来定义的。由于一阶逻辑模型数量没有上限,因此无法通过枚举所有模型的方式来检验蕴含。即便对象的数量是有限的,其组合也会是巨量的。
当有了支持对象的逻辑后,就很自然地想要表达很多对象的整体属性而非根据名称逐个列举对象。量词能达到这一目的。一阶逻辑含有两个标准量词——全称量词和存在量词。
当两个量词与相同的变量名合用时会引起一些混淆。规则是,变量属于提及它的最内层量词,随后便不再受任何其他量词约束。通常来说始终会在嵌套量词中使用不同的变量名。
量化语句和非量化语句的德摩根律如下:
此外全称量词通常与蕴涵式搭配防止断言过强,反之存在量词通常与合取式搭配防止断言过弱。
首先,确定每个常量符号都指代一个唯一的对象——唯一名称假设。然后,假设未知其为真的原子语句事实上都为假——封闭世界假设。最后,调用域闭包,意味着每个模型中的域元素不多于常量符号指代的那些。在由此产生的语义中称之为数据库语义,以区别于标准的一阶逻辑语义。
逻辑中不存在“正确的”语义,提出的语义的有用性取决于它对人类想要记录的知识的表示是否简洁和直观,以及相应的推断规则的生成是否容易和自然。当明确了知识库中描述的所有对象的身份,并且掌握了所有事实的时候,数据库语义最有用,它大大少于标准一阶逻辑语法下巨量的模型数量。不过,数据库语义需要世界中包含的东西的确定知识。而在其他情况下,数据库语义就很棘手。
一阶逻辑的使用
语句是通过$Tell$添加到知识库的,与在命题逻辑中完全一样,这种语句被称为断言。使用$Ask$提出的问题被称为查询或目标。一般来说,知识库中逻辑蕴含的所有查询都应该得到肯定的回答。
如果想了解使语句为真的$x$的值,就需要另一个函数$AskVars$,语句返回$\left\{ x/常量 \right\} $形式的结果,这种回答叫作置换或绑定表。
命题推断
进行一阶推断的方法之一是将一阶知识库转换为命题逻辑并使用已知的命题推断。第一步是消去全称量词,一般来说,全称量词实例化表明可以通过用基本项(没有变量的项)置换全称量化的变量来推断任意语句。使用置换(绑定表)来形式化地写出推断规则,令$Subst\left( \theta ,\alpha \right) $表示对语句$\alpha $应用置换$\theta $后的语句。则对于任意变量$v$和基本项$g$,规则写作:
$$
\frac{\forall v\ \alpha}{Subst\left( \left\{ v/k \right\} ,\alpha \right)}
$$
类似地,存在量词实例化用一个新的常量符号替换存在量化的变量。其形式化描述如下:对于任意语句$\alpha $、变量$v$和未在知识库其他地方出现的常量符号$k$:
$$
\frac{\exists v\ \alpha}{Subst\left( \left\{ v/k \right\} ,\alpha \right)}
$$
简单来说,存在语句表明存在满足某个条件的对象,运用存在实例化就是给这个对象命名。当然,这个名称不能已经属于其他对象。在逻辑中,新的名称被称为斯科伦常量。
全称量词实例化可以多次用于同一条公理来产出许多不同结果,而存在量词实例化只需要使用一次,随后就可以丢掉存在量化的语句。
这种命题化技术可以被彻底一般化。然而,如果知识库中包含函数符号,可能的基本项置换集是无穷的,比如可以构造无穷多的嵌套项。幸运的是,雅克·埃尔布朗针对这一现象提出了著名的定理,即如果语句被原始的一阶知识库蕴含,则存在仅涉及命题化知识库的有限子集的证明。由于任意这样的子集都有其基本项的最大嵌套深度,可以通过先生成含有常量符号的所有实例化,然后再生成深度为$1$的所有项,然后是深度为$2$的所有项,以此类推,直到能够构建所蕴含语句的命题证明。
以上就是通过命题化进行一阶逻辑推断的完备方法,也就是,所有蕴含的语句都可以被证明。这是一个重大的成就,特别是在可能模型的空间无限大的情况下。但是,在证明完成前并不知道语句是被蕴含的!如果语句并不被蕴含怎么办?能证明吗?实际上,对于一阶逻辑,答案是否定的。证明程序会一直运行,生成越来越深的嵌套项,但不知道它是陷入绝望的循环,还是就快要得出证明结果。
一阶逻辑的蕴含问题是半可判定的,也就是,存在能判定所有蕴含的语句的算法,却不存在能够判定所有不蕴含的语句的算法。