红黑树
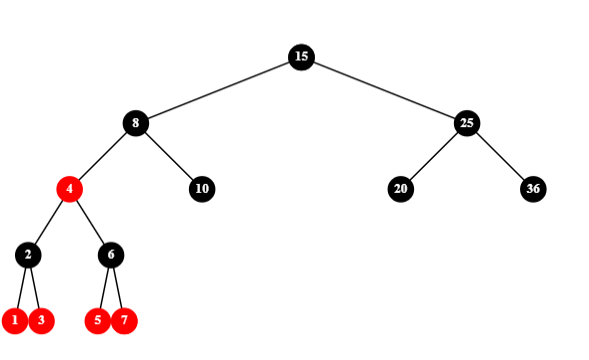
红黑树的插入有 12 种情况,插入一个结点最容易出现两个连续的红色结点从而破坏红黑树的性质,故需要进行双红调整。插入的情况整体分为三类,第一类是父节点为黑节点直接插入:
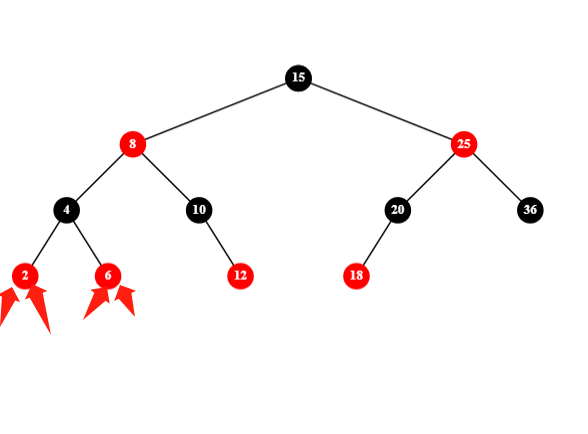
第二种情况是父节点为红色且父节点有兄弟:
这种只需要将父节点和叔父节点染黑,然后沿路径递归染色即可:
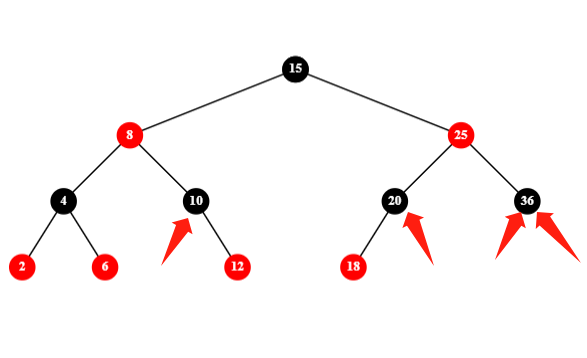
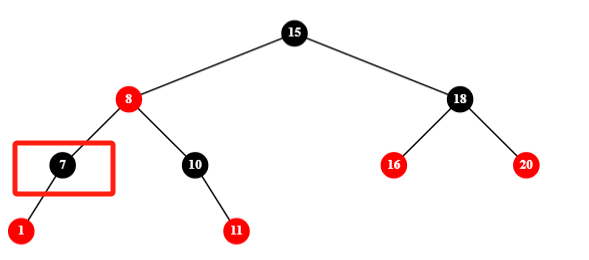
第三种情况是父节点为红色且父节点无兄弟:
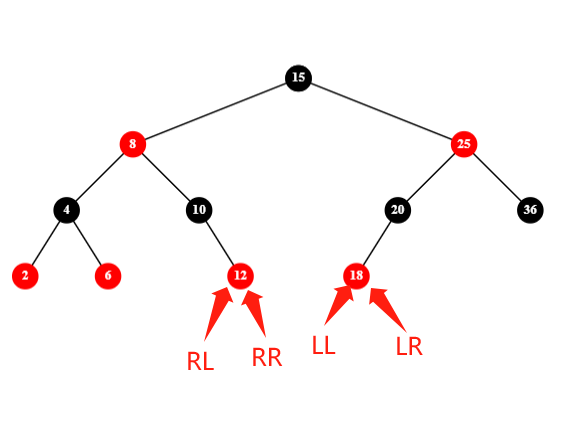
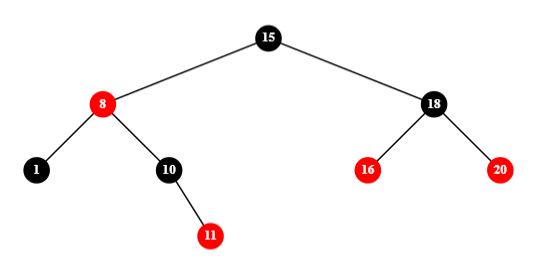
LL/RR 的情况是父节点染为黑色,然后右/左旋:
RL/LR 的情况是父节点右/左旋,父节点左/右旋,然后染色:
删除操作,最容易造成子树黑高(Black Height)的变化(删除黑色结点可能导致根结点到叶结点黑色结点的数目减少,即黑高降低),从而需要进行双黑调整,双黑修正过程总共耗时不超过$O(logn)$。即便计入此前的关键码查找和节点摘除操作,红黑树的节点删除操作总是可在$O(logn)$时间内完成。
首先需要知道,对于非叶子节点的删除,首先要转化为非叶子节点的删除,即用直接前驱或者直接后继替换以后删除叶子节点。对叶子节点的删除整体上可以分为两类:
第一类是对红色节点的删除,此类节点可以直接删除;
第二类是对黑色节点的删除,此类又可以细分为三类,
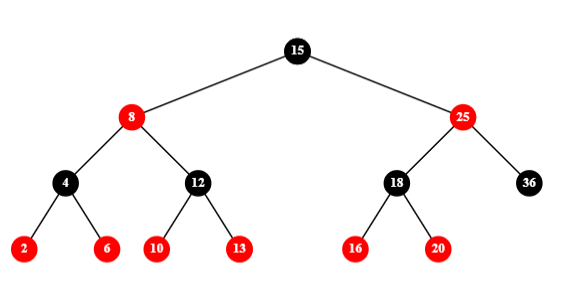
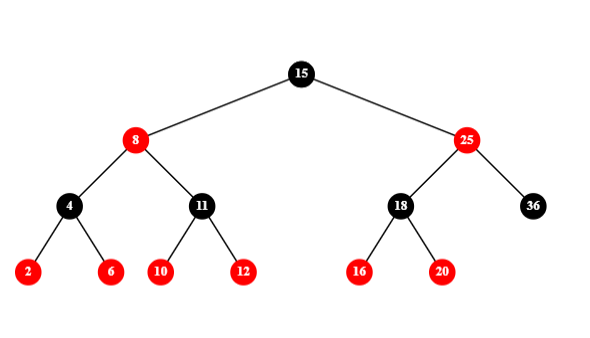
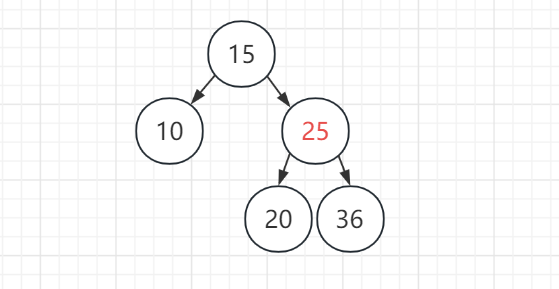
1)有两个红色子节点的黑色节点,此类其实不存在,其可以转化为对其子节点的删除:
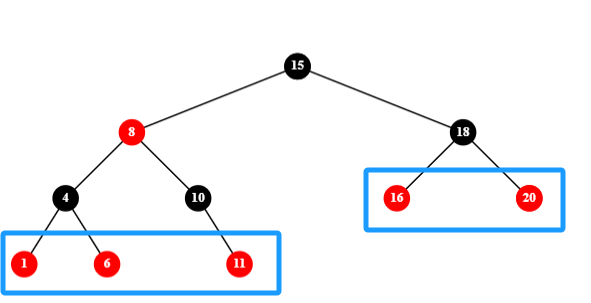
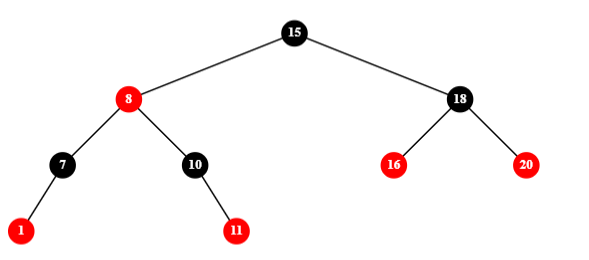
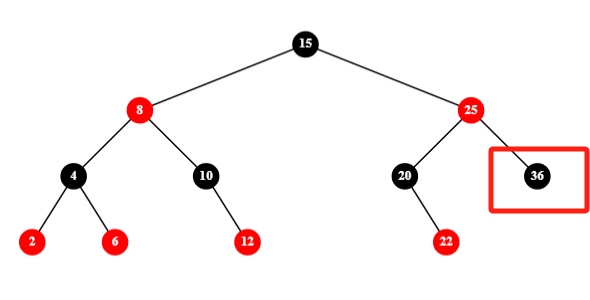
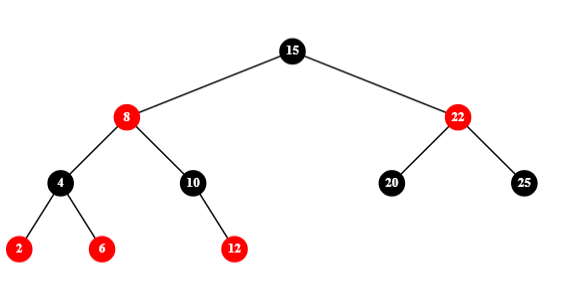
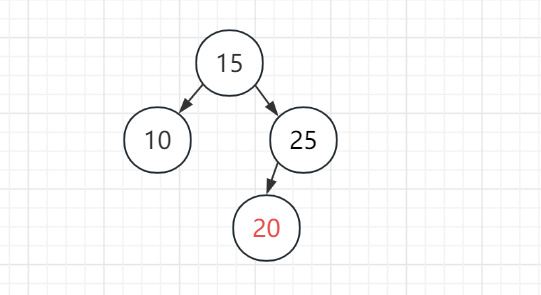
2)有一个红色子节点的黑色节点,将唯一子节点替代黑色节点并染为黑色:
3)黑色叶子节点,这又分为三种情况:
1、删除节点为根节点,直接删除;
2、删除节点的兄弟节点是黑色节点,此出又分为两种情况:
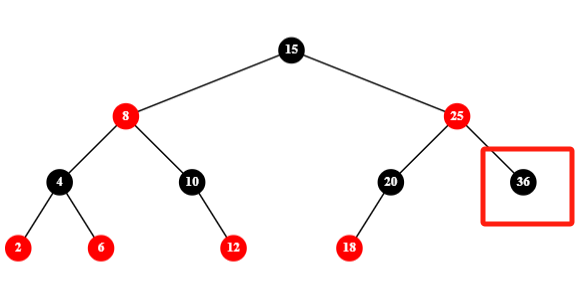
1-兄弟节点有红色子节点,这里再细分为三种情况:
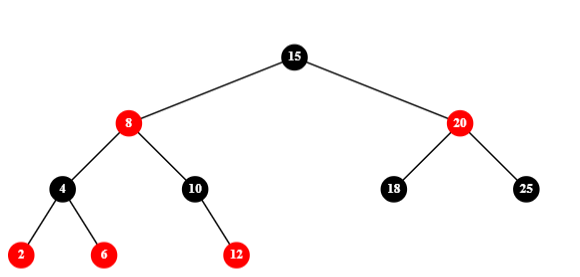
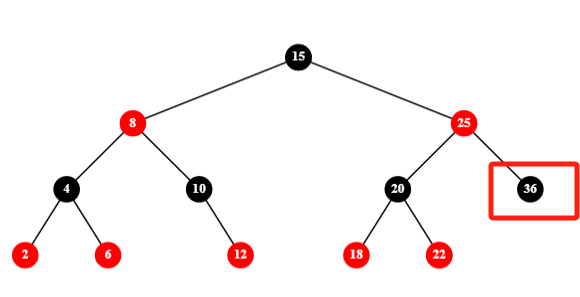
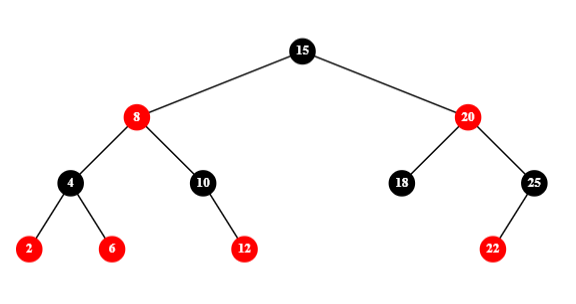
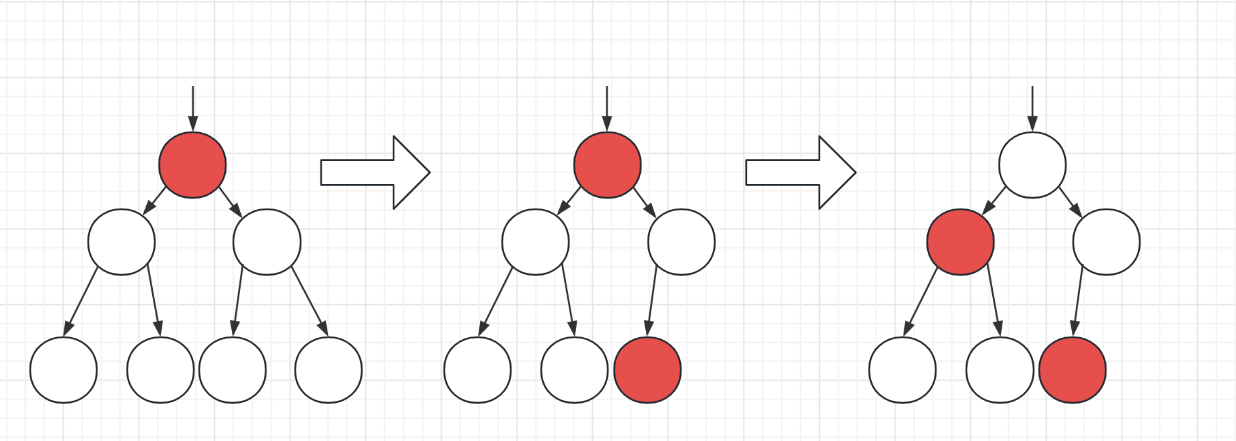
-1-兄弟节点有左红子节点,删除节点的父节点(LL)右旋,删除节点的兄弟节点替代其父节点染为红色,向下染黑:
-2-兄弟节点有右红子节点,相当于是 LR 旋转,实质上是中间值化为父节点,即兄弟节点先左旋父节点右旋,中间值替代染为红色,子节点染为黑色:
-3-兄弟节点有双红子节点,最简单是父节点 LL 右单旋,兄弟节点替代父节点染为红色,向下递归染黑染红:
2-兄弟节点没有红色子节点,这里再细分为两种情况:
-1-父节点是红色,位置不发生变化,父节点染黑,向下递归改色:
-2-父节点是黑色,兄弟染为红色,进而影响祖父黑高故对父节点再次进行双黑调整,即变成父节点为红色兄弟节点没有红色子节点的调整,即父节点染为黑色,兄弟节点染为红色:
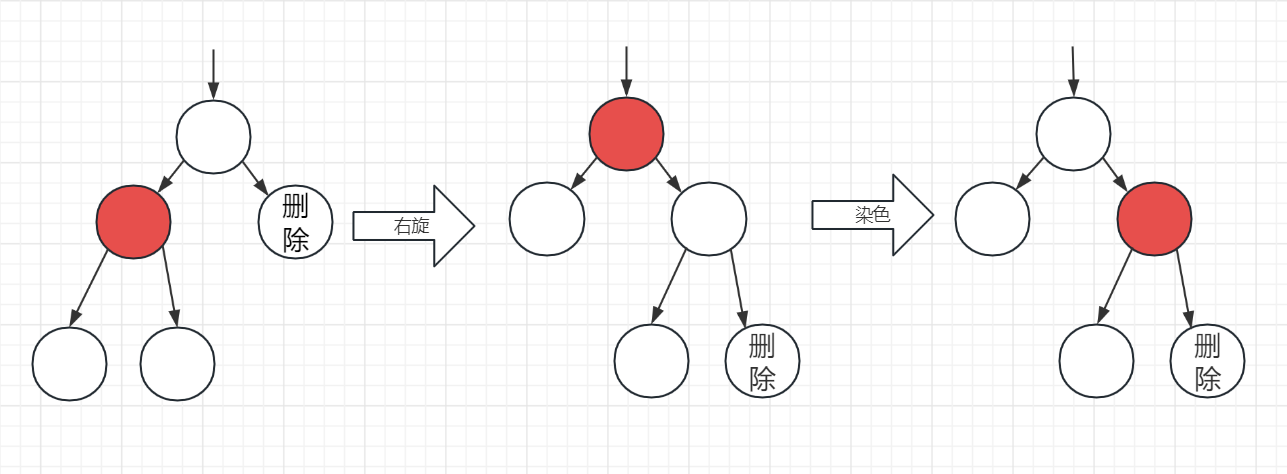
3、删除节点的兄弟节点是红色节点,转变为兄弟节点为黑色来处理,先将父节点右旋,兄染黑,父染红:
思维导图如下:
思维导图源文件$kd$-树
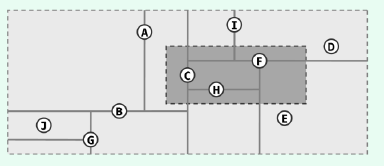
$kd$-$tree$是$K$-$dimension$ $tree$的缩写,是对数据点在$k$维空间中划分的一种数据结构。本质上,$kd$-树是一种空间划分树,是一种平衡二叉树。将整个$k$维的向量空间不断的二分,从而划分为若干局部空间,然后搜索的时候,不断进行分支判断,选择其中的局部子空间,避免了全局空间搜索。以下是一个二维情形的划分:
$kd$-树的构建流程:
1. 选择维度:$kd$-树建树采用的是从$m$个样本的$n$维特征中,分别计算$n$个特征的取值的方差,用方差最大的第$k$维特征 来作为根节点。
2.选择中位数:对于这个特征,选择特征的取值的中位数$v$对应的样本作为划分点;
3. 分割数据:对于所有第$k$维特征的取值小于$v$的样本,划入左子树,对于第$k$维特征的取值大于等于$v$的样本,划入右子树。
4. 递归迭代:对于左子树和右子树,采用和刚才同样的办法来找方差最大的特征来做更节点,将空间和数据集进一步细分,如此直到所有点都被划分。