推断与证明
首先介绍可以用于推导证明的推断规则。证明是一系列可以引向所需目标的结论。最著名的规则是肯定前件,写作:
$$
\frac{\alpha \Rightarrow \beta \text{,}\alpha}{\beta}
$$
意为给定$\alpha $和具有$\alpha \Rightarrow \beta $形式的语句时,可以推导出语句$\beta $。另一个有用的推断规则是合取消去,即可以从一个合取式推导出任一合取子句:
$$
\frac{\alpha \land \beta}{\alpha}
$$
这些规则可用于任意适用的实例,不必枚举所有模型就可以生成可靠的推断。应用任意搜索算法都可以找到构成证明的一系列步骤。只需要定义如下的证明问题:
初始状态:最初的知识库。
动作:动作的集合,它包含所有推断规则应用于所有符合上半部分推断规则的语句。
结果:一个动作的结果是将推断规则下半部分的语句实例加入知识库。
目标:目标是含有试图证明的语句的状态。
这样,搜索证明就可以替代枚举模型。在许多实际案例中,找出某种证明的效率更高,因为证明可以忽略许多无关的命题,不论这种命题有多少。即使在知识库中再添加一百万条语句,这一结果依然成立。而简单的真值表算法将无法承受这种模型的指数级爆炸式增长。
逻辑系统的最后一个属性是单调性,它表明蕴含的语句集只能随着信息被加入知识库而增长。单调性意味着只要在知识库中找到合适的前提,就可以使用推断规则——规则的结论必然是合理的,不论知识库中还有什么东西。
$$
\text{如果}KB\models \alpha \text{则}\left( KB\land \beta \right) \models \alpha
$$
使用归结证明
归结与任意完备的搜索算法结合后,可以产生一个完备的推断算法。首先是单元归结:
$$
\frac{\ell _1\lor \cdot \cdot \cdot \lor \ell _k,\ \ \ m}{\ell _1\lor \cdot \cdot \cdot \ell _{i-1}\lor \ell _{i+1}\cdot \cdot \cdot \lor \ell _k}
$$
其中每个$\ell $都是文字,而$\ell _i$和$m$是互补文字(即各自是对方的否定)。这样,单元归结推断规则使用一个子句(文字的析取式)以及一个文字,生成一个新的子句。注意,单个文字可看作是一个文字的析取式,也被称为单元子句。单元归结规则可以推广为全归结规则:
$$
\frac{\ell _1\lor \cdot \cdot \cdot \lor \ell _k,\ \ \ m_1\lor \cdot \cdot \cdot m_n}{\ell _1\lor \cdot \cdot \cdot \ell _{i-1}\lor \ell _{i+1}\cdot \cdot \cdot \lor \ell _k\lor m_1\lor \cdot \cdot \cdot m_{j-1}\lor m_{j+1}\cdot \cdot \cdot \lor m_n}
$$
其中,$\ell_i$和$m_j$是互补文字。这表明归结使用两个子句并产生一个新的子句,该新子句包含除一对互补文字以外的原始子句的所有文字。注意,一次只归结一对互补文字。归结规则还有一个技术细节:结果子句只能含有每个文字的一个副本。去除文字的多个副本被称为因子提取。例如,如果我们用$A\lor \lnot B$归结$A\lor B$,得到$A\lor A$,通过因子提取简化为$A$。
归结的有效性很容易证明,若假定$\ell_i$为真则$m_j$为假,故易有$m_1\lor \cdot \cdot \cdot m_{j-1}\lor m_{j+1}\cdot \cdot \cdot \lor m_k$为真。因此无需考虑其他部分,易知$\ell _1\lor \cdot \cdot \cdot \ell _{i-1}\lor \ell _{i+1}\cdot \cdot \cdot \lor \ell _k\lor m_1\lor \cdot \cdot \cdot m_{j-1}\lor m_{j+1}\cdot \cdot \cdot \lor m_k$。归结法则最重要的部分在于,它形成了一类完备推断过程的基础。基于归结的定理证明器可以对命题逻辑中的任意语句$\alpha $和$\beta $确定$\alpha \models \beta $是否成立。
归结规则仅适用于子句(也就是文字的析取式),因此它似乎只能用于含有子句的知识库和查询。那么对于所有命题逻辑,它如何实现完备的推断过程?答案是,命题逻辑的所有语句逻辑上都等价于子句合取式。形式为子句合取式的语句被称为合取范式或$CNF$。将任意语句逻辑转换为$CNF$的过程为:
1、消去$\Leftrightarrow $:
$$
\alpha \Leftrightarrow \beta =\left( \alpha \Rightarrow \beta \right) \land \left( \beta \Rightarrow \alpha \right)
$$
2、消去$\Rightarrow $:
$$
\alpha \Rightarrow \beta =\lnot \alpha \lor \beta
$$
3、$CNF$要求$\lnot $只能在文字前出现,因此反复应用如下的等价关系“将$\lnot $内移”:
4、不断应用分配律将$\land $和$\lor $配对形成$CNF$。
通过以上操作,原始语句现在已经成为$CNF$,是多个子句的合取式。它读起来难了很多,但它可以作为归结过程的输入。
欲证$\alpha \models \beta $只需要证$\alpha \land \lnot \beta $是不可满足的,具体证明过程为:
$Step1$:将$\alpha \land \lnot \beta $转换为$CNF$;
$Step2$:归结规则应用在得到的子句上。每一对互补文字都被归结生成新的子句,如果新子句没有出现过,就将其加入子句集合。
$Step3$:若此时没有可供添加的新子句,则判断$KB$不蕴含$\alpha $;若两个子句归结为空子句,则判断$KB$蕴含$\alpha $;否则转$Step2$。
空子句是一个没有析取子句的析取式,它等价于$False$,因为仅当至少一个析取子句为真时析取式为真。另外,空子句仅在归结两个矛盾的单元子句时出现。
首先引入子句集合$S$的归结闭包$RC(S)$,即对$S$中子句及其生成子句反复使用归结规则可推得的所有子句的集合。易知$RC(S)$必然是有限的:得益于因子提取,由$S$中出现的符号$P_1,…, P_k$得出的子句数量是有限的。因此,归结算法总是能够终止。命题逻辑中归结的完备性定理被称为基本归结定理:
如果一个子句集是不可满足的,则这些子句的归结闭包含有空子句。
定理的证明是通过其假言易位进行的:如果闭包$RC(S)$不含有空子句,则$S$可满足,即证明闭包$RC(S)$不含有空子句时所有子句都是$True$。首先构造如下指派$m$:若$RC(S)$包含一个子句,该子句包含$\lor \lnot R_i$,且该子句中的其他文字都已被指派为$False$,则将$R_i$指派为$False$,否则将$R_i$指派为$True$。假设在对$R_i$的指派导致$RC(S)$中首次出现为$False$的子句,则该子句必然为如下两种形式之一:
$$
false\lor false\lor \cdot \cdot \cdot false\lor R_i
$$
$$
false\lor false\lor \cdot \cdot \cdot false\lor \lnot R_i
$$
若$RC(S)$仅包含上面两种形式的其中一种,则指派$R_i$后,必然不会出现$False$的子句。因此,$RC(S)$同时包含上述两种形式。由归结原理,它们归结的子句也应该在$RC(S)$中,则该子句已经为$False$,这与“对$R_i$的指派导致$RC(S)$中首次出现为$False$的子句”矛盾。
因此,证明了这种构建永远无法使$RC(S)$中的子句为假,也就是说它创建了一个$RC(S)$的模型。最后,由于$S$包含在$RC(S)$中,因此任意$RC(S)$的模型也是$S$本身的模型。
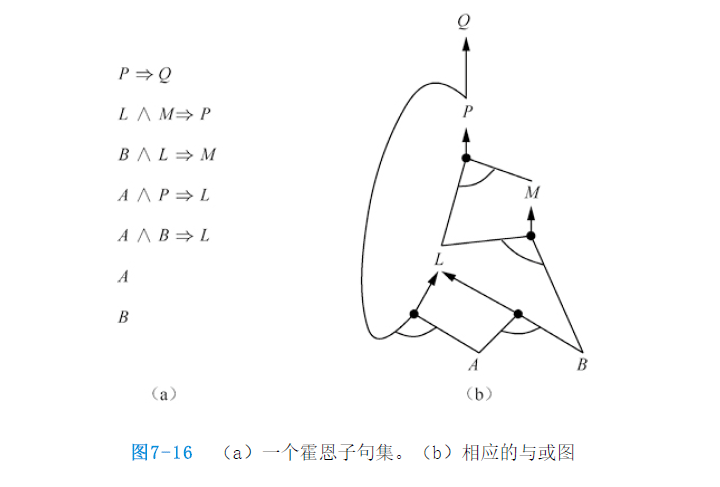
霍恩子句与确定子句
归结的完备性使其成为一种非常重要的推断方法。而许多实际情形并不需要用到归结的全部能力。一些真实世界的知识库中的语句满足某些限制,这使得它们可以使用更为受限而更高效的推断算法。其中一种受限形式是确定子句,它是文字的析取式,其中只有一个为正文字。
更一般性的是霍恩子句,它是文字的析取式,其中最多只有一个为正文字。因此所有的确定子句都是霍恩子句,没有正文字的子句也是霍恩子句——也被称为目标子句。霍恩子句在归结时是闭的:如果归结两个霍恩子句,仍然会得到霍恩子句。还有一种类型是$k$-$CNF$语句,它是每个子句最多含有$k$个文字的$CNF$语句。
仅含有确定子句的知识库很有意义,原因有 3 个:
1、每个确定子句都可以写成一个蕴涵式,前提是正文字的合取式,结论是一个正文字。例如,确定子句$\left( \lnot A\lor \lnot B\lor C \right) $可以写作$\left( A\land B \right) \Rightarrow C$。在霍恩形式中,前提被称为体而结论被称为头。
2、用霍恩子句进行推断可以通过前向链接算法和反向链接算法完成,这些算法都很自然,因为它们的推断步骤很直观,便于人类理解。
3、用霍恩子句确定蕴含关系所需的时间与知识库大小呈线性关系,这格外令人满意。
前向链接与反向链接
前向链接算法确定单个命题符号$q$(即查询)是否被确定子句的知识库所蕴含。它从知识库中的已知事实(正文字)开始。如果一个蕴涵式的所有前提都已知,则将其结论添加到已知事实的集合中。这一过程持续进行,直到查询$q$被添加,或直到无法进一步进行推断,它的运行时间是线性的。
显然,前向链接是可靠的:每个推断实际上都是对肯定前件的运用。前向链接也是完备的:所有蕴含的原子语句都将被推得。
完备性证明:考察算法达到不动点时的状态,即不会再出现新的推理(因为子句集是有限的,故其可以归结出的子句也是有限的;又推理算法具有单调性,所以一定会达到这个不动点。此时将所有被推导出的语句设为$True$(因为前向链接是可靠的),未被推导出的语句记为$False$。再证明原始$KB$的所有语句在该不动点子句集中为真。
反证:假设存在$KB$中某个子句$a_1\land a_2\land …\land a_k\Rightarrow b$在该不动点子句集中为假(也就是说该子句未被推导出来),那么$a_1\land a_2\land …\land a_k$必为真,$b$必为假,$a_1\land a_2\land …\land a_k$应该被推导出来。这与算法到达了不动点矛盾。更进一步,被$KB$蕴含的$q$在不动点子句集下也一定为真,所以一定会被推导出来。
前向链接是数据驱动推理这一更广泛概念的例子,也就是其注意力开始集中在已知数据的推理。它可以用于智能体,以便从收到的感知推导出结论,且常常是在没有特定查询的情况下。对人类来说,当获取新信息后会出现一定数量的数据驱动推理。例如,如果在屋子里听到外面开始下雨,则可能会想到取消野餐;但是,大概不会想到邻居花园里最大的一朵玫瑰的第 17 片花瓣会淋湿——人类会对前向链接进行精心地控制,以免被无关的结果淹没。
反向链接算法如其名称所示,从查询开始反向运作。如果查询$q$已知为真,则不需要做任何操作。否则,算法将在知识库中找寻结论为$q$的蕴涵式。如果这些蕴涵式的所有前提都可以(用反向链接)证明为真,则$q$为真。与前向链接一样,它的高效实现的时间复杂性是线性的。
反向链接是一种目标导向推理。它对于回答类似“我现在该做什么?”和“我的钥匙在哪里?”这样的特定问题非常有用。通常,反向链接的代价远小于知识库规模的线性变化,因为这个过程仅涉及相关的事实。