伸展树
伸展树($splay$ $tree$)也是平衡二叉搜索树的一种形式。相对于$AVL$树,伸展树的实现更为简捷。伸展树无需时刻都严格地保持全树的平衡,但却能够在任何足够长的真实操作序列中,保持分摊意义上的高效率。伸展树也不需要对基本的二叉树节点结构,做任何附加的要求或改动,更不需要记录平衡因子或高度之类的额外信息,故适用范围更广。
信息处理的典型模式是,将所有数据项视作一个集合,并将其组织为某种适宜的数据结构,进而借助操作接口高效访问。现实中,通常在任意数据结构的生命期内,不仅执行不同操作的概率往往极不均衡,而且各操作之间具有极强的相关性,并在整体上多呈现出极强的规律性。其中最为典型的,就是所谓的“数据局部性”,这包括两个方面的含义:
1)刚刚被访问过的元素,极有可能在不久之后再次被访问到;
2)将被访问的下一元素,极有可能就处于不久之前被访问过的某个元素的附近;
充分利用好此类特性,即可进一步地提高数据结构和算法的效率。就二叉搜索树而言,数据局部性具体表现为:
1)刚刚被访问过的节点,极有可能在不久之后再次被访问到;
2)将被访问的下一节点,极有可能就处于不久之前被访问过的某个节点的附近;
因此,只需将刚被访问的节点,及时地“转移”至树根(附近),即可加速后续的操作。当然,转移前后的搜索树必须相互等价。
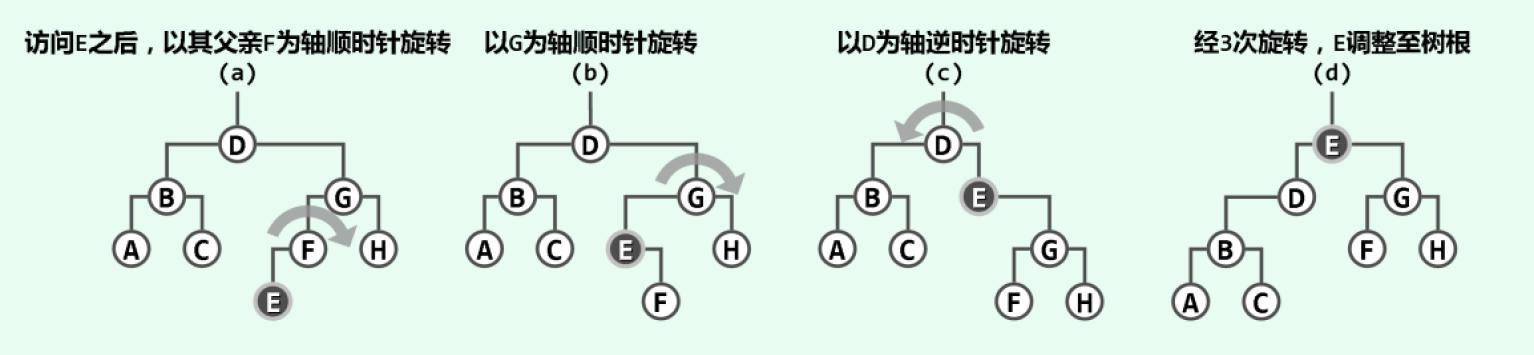
一种直接方式是:每访问过一个节点之后,随即反复地以它的父节点为轴,经适当的旋转将其提升一层,直至最终成为树根。
随着节点$E$的逐层上升,两侧子树的结构也不断地调整,故这一过程也称作伸展,而采用这一调整策略的二叉搜索树也因此得名。不过,为实现真正意义上的伸展树,还须对以上策略做点微妙而本质的改进。之所以必须改进,是因为目前的策略仍存在致命的缺陷,对于很多访问序列,单次访问的分摊时间复杂度在极端情况下可能高达$\varOmega \left( n \right) $。
为克服上述伸展调整策略的缺陷,一种简便且有效的方法就是:将逐层伸展改为双层伸展。具体地,每次都从当前节点$v$向上追溯两层(而不是仅一层),并根据其父亲$p$以及祖父$g$的相对位置,进行相应的旋转。以下分三类情况,分别介绍具体的处理方法。
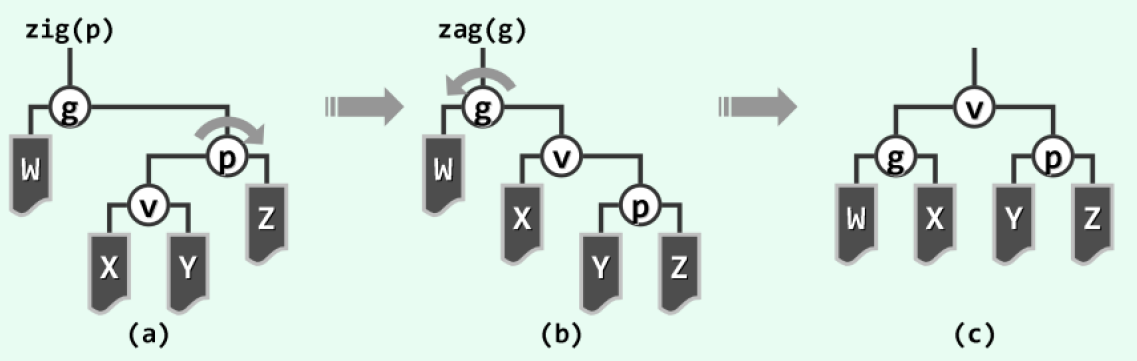
第一种情况是 LL 右双旋或 RR 左双旋,先祖父后父节点,两者对称:
第二种情况是 RL 右左双旋或 RR 左右双旋,先父节点后祖父,两者对称:
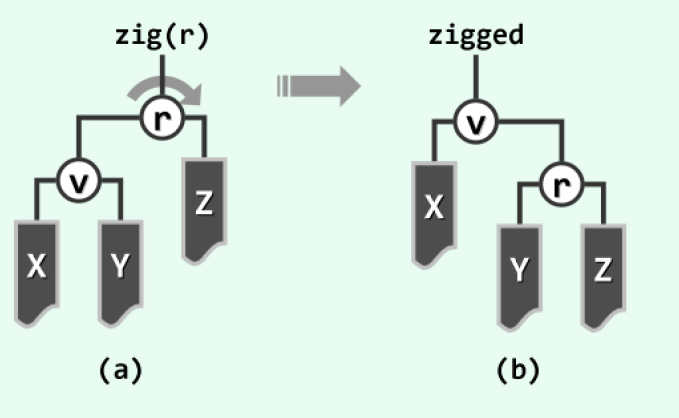
前两者为将节点上推两层,接下来第三种情况则是往上一层,此时树高为 2,调整后成为根:
Tarjan 等人采用势能分析法已证明,在改用“双层伸展”策略之后,伸展树的单次操作均可在分摊的$O(logn)$时间内完成。
在伸展树中查找任一关键码$e$的过程:首先,调用二叉搜索树的通用算法尝试查找具有关键码$e$的节点。无论查找是否成功,都继而调用$splay()$算法,将查找终止位置处的节点伸展到树根。
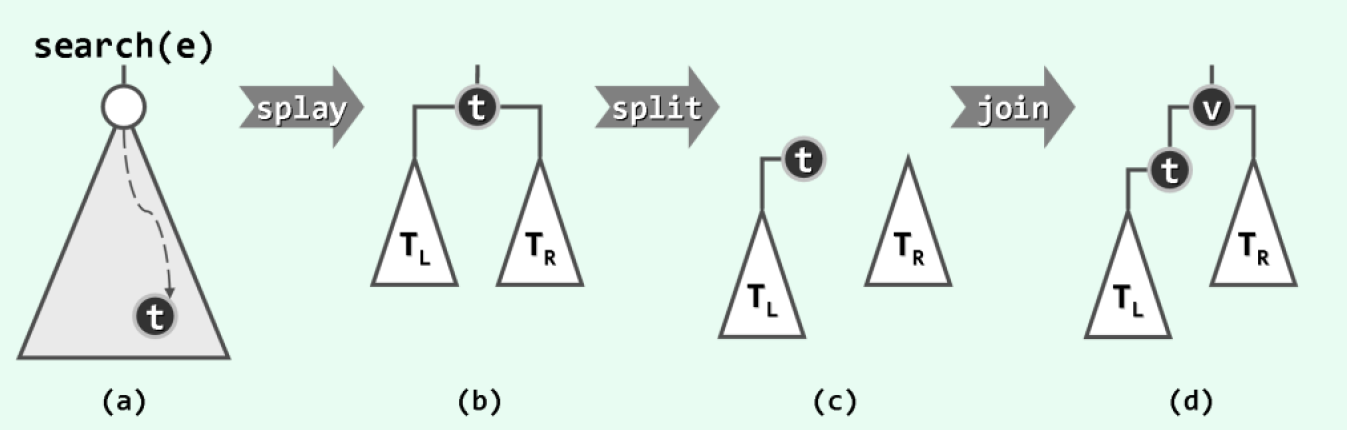
为将关键码$e$插至伸展树$T$中,首先调用伸展树查找接口,查找该关键码,将最后被访问的节点$t$通过伸展被提升为树根,其左、右子树分别记作$T_L$和$T_R$。接下来,根据$e$与$t$的大小关系(不妨排除二者相等的情况),以$t$为界将$T$分裂为两棵子树。比如,不失一般性地设$e$大于$t$。于是,可切断$t$与其右孩子之间的联系,再将以$e$为关键码的新节点$v$作为树根,并以$t$作为其左孩子,以$T_R$作为其右子树:
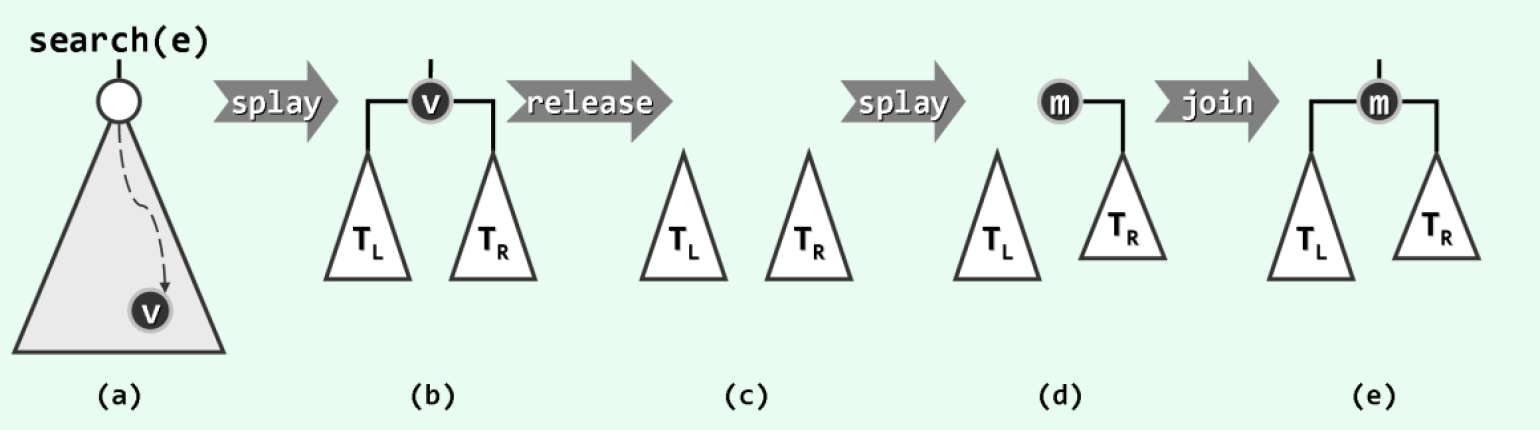
为从伸展树$T$中删除关键码为$e$的节点,首先亦调用接口查找该关键码,且不妨设命中节点为$v$。于是,$v$将随即通过伸展被提升为树根,其左、右子树分别记作$T_L$和$T_R$。接下来,将$v$摘除。然后,在$T_R$中再次查找关键码$e$。尽管这一查找注定失败,却可以将$T_R$中的最小节点$m$,伸展提升为该子树的根。
得益于二叉搜索树的顺序性,此时节点$m$的左子树必然为空;同时,$T_L$中所有节点都应小于$m$。于是,只需将$T_L$作为左子树与$m$相互联接,即可得到一棵完整的二叉搜索树。如此不仅删除了$v$,而且既然新树根$m$在原树中是$v$的直接后继,故数据局部性也得到了利用。
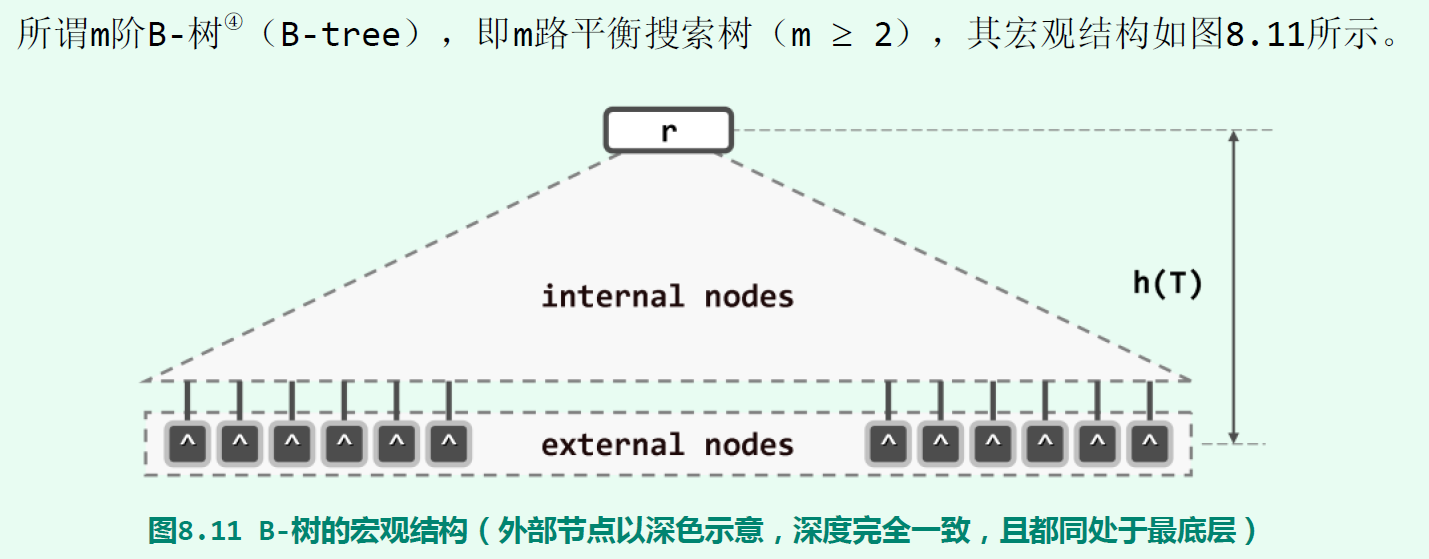
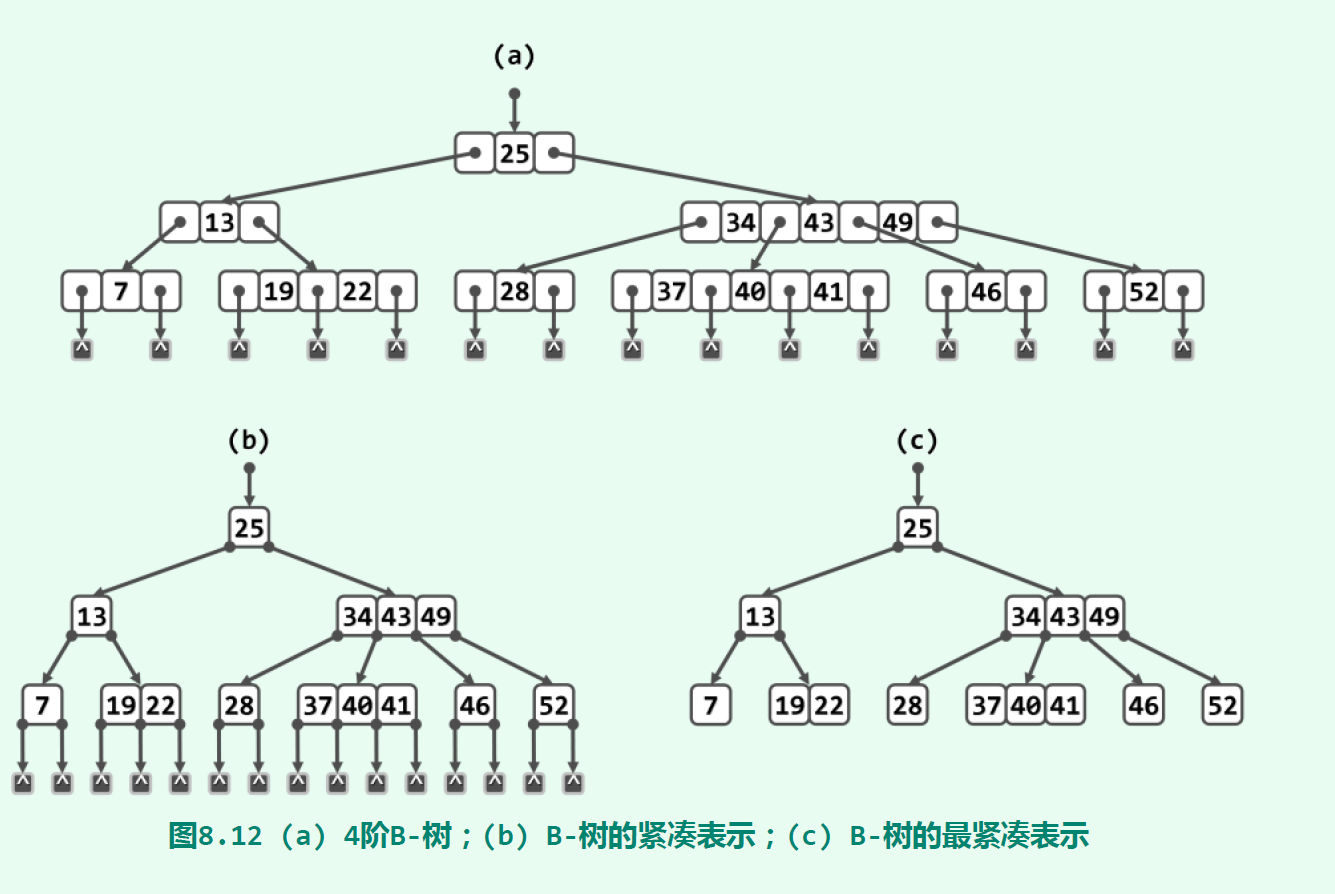
$B$树
其中,所有外部节点均深度相等。同时,每个内部节点都存有不超过$m$-$1$个关键码,以及用以指示对应分支的不超过$m$个引用。树高满足条件:$\log _m\left( n+1 \right) \le h\le \log _{\lceil m/2 \rceil}\left( \frac{n+1}{2}+1 \right) $,除根以外的所有内部节点,都应满足:$n+1\ge \lceil m/2 \rceil $;在非空的$B$-树中,根节点应满足:$n+1\ge 2$。含有$n$个非叶节点的$m$阶$B$树至少包含$\left( n-1 \right) \left( \lceil m/2 \rceil -1 \right) +1$个关键字。
$B$-树的插入:
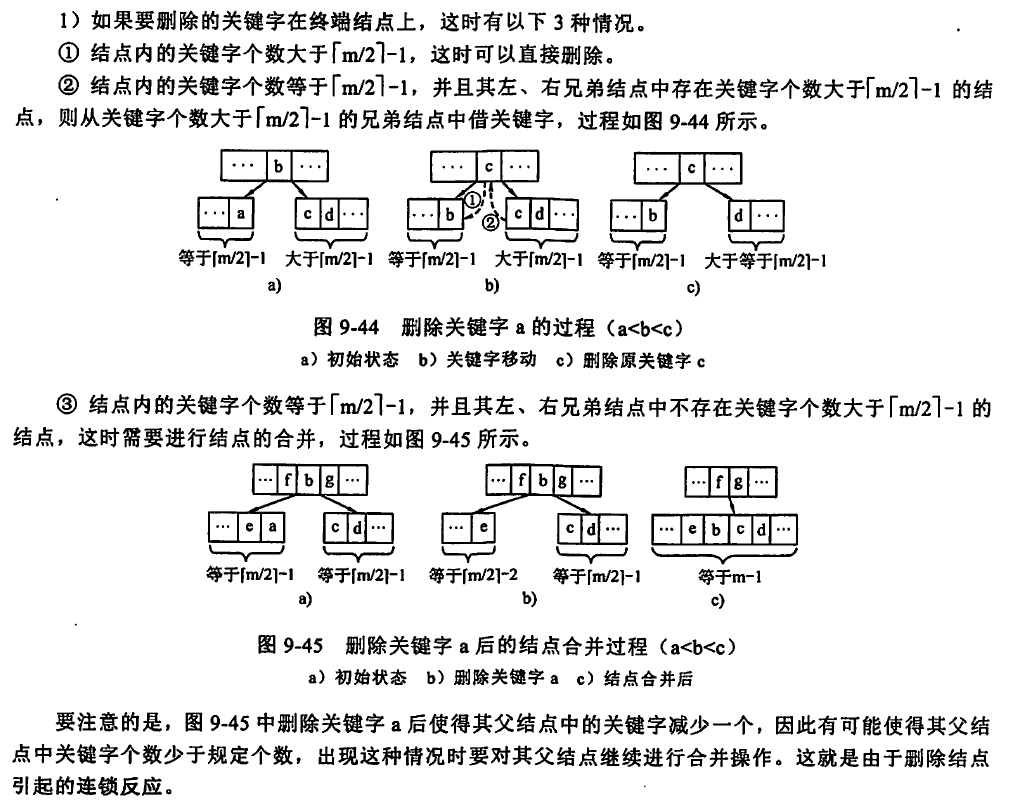
$B$-树的删除:
若被删除关键字在非终端节点,则用直接前驱或直接后继来替代被删除的关键字。直接前驱: 当前关键字左侧指针所指子树中“最右下”的元素;直接后继:当前关键字右侧指针所指子树中“最左下”的元素,然后再按前面所述方法进行处理。