非确定性动作的搜索
当环境部分可观测时,智能体并不确定它处于什么状态;当环境是非确定性的时,智能体不知道在执行某个动作后将转移到什么状态。这意味着智能体所思考的不再是“我现在位于$s_1$状态,如果我执行$a$动作,我将会进入$s_2$状态”,而是“我现在位于$s_1$或$s_3$状态,如果我执行$a$动作,我将会进入$s_2$、$s_4$或$s_5$状态”。通常把智能体认为其可能位于的物理状态集合称为信念状态。
在部分可观测的和非确定性的环境中,问题的解不再是一个序列,而是一个条件规划(有时也称为应变规划
或策略),条件规划根据智能体在执行规划时接收到的感知来指定动作。
如果环境是完全可观测的、确定性的和完全已知的,那么使用之前提到过的的任意算法都很容易求解这个问题,它的解是一个动作序列。假设环境的不确定性由智能体的动作所带来,为了更好地形式化这类问题,需要对之前的转移模型进行推广,不使用返回单个结果状态的$Result$函数来定义转移模型,而是使用返回一组可能的结果状态的新的$Result$函数。
在这种情况下,没有任何一个单独的动作序列能够求解问题,因此需要使用条件规划作为问题的解,条件规划可以包含$if$–$then$–$else$步骤;这意味着解是树而不是序列。这里的$if$语句中的条件用来测试当前状态;这是智能体在运行时能够观测到的,但规划时还不知道。
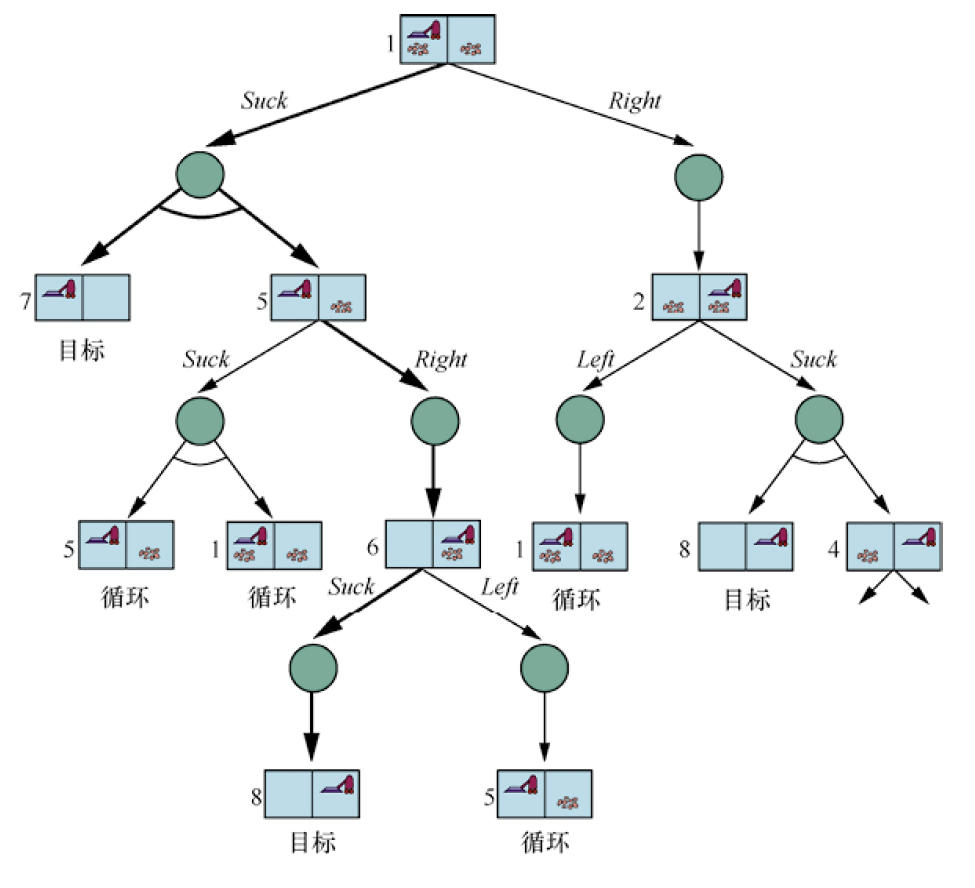
如何对这些非确定性问题的进行求解,和其他算法一样,首先从构造搜索树开始,但是求解这类问题的树有一个不同的特性。在确定性环境中,分支是由智能体在每个状态下自己的选择引入的,称这些节点为或节点($OR$ $node$)。而在非确定性环境中,环境对每个动作的结果的选择也会引入分支,称这些节点为与节点($AND$ $node$)。这两种节点交替出现,形成与或树($AND$–$OR$ $tree$)。以下是个示例:
与节点(用圆圈表示)上的每个结果都必须处理,结果分支间用弧线连接,找到的解用粗线标识。与或搜索问题的解是完整搜索树的一棵子树:(1)每个叶子都是一个目标节点,(2)在每个或节点上选择一个动作,(3)每个与节点包括所有结果分支。解在图中用粗线标识。
与或图搜索的通常做法是深度优先递归,该算法的一个关键是它处理环的方法,环经常出现在非确定性问题中。如果当前状态与从根到它的路径上的某个状态相同,就返回失败。
这并不意味着从当前状态出发没有解;这仅仅意味着,如果存在一个非循环解,那么它肯定可以从当前状态的早期镜像到达,因此可以丢弃新的镜像。有了这一检查,可以确保算法在任何有限状态空间中都能终止,因为每条路径都必定到达一个目标、一个死胡同或一个重复状态。注意,该算法并不检查当前状态是否是从根出发的其他路径上的某个状态的重复状态,这一点对效率来说很重要。
在操作有时会失效的情况下,$And$-$Or$-$Search$在不允许循环解的情况下将经常返回失败。然而,存在一个循环解,即反复尝试执行动作,直到它生效,可以用一个 while 结构来表示这一过程。
可以考虑将循环规划作为解的最小条件是每个叶节点都是一个目标状态,并且叶节点可以从规划中的任意点到达。除此之外,还要考虑造成非确定性的原因。如果确实是动作重复足够多次,最终总会生效的话,规划便也会成功。但是,如果这种非确定性来自机器人或环境的一些尚未观测到的原因,重复这个动作也没有用。
部分可观测环境中的搜索
当智能体的感知根本不提供任何信息时,问题就变成了无传感器问题,或称一致性问题。乍一看如果无传感器智能体不知道起始状态,那它就无法求解问题,但出人意料的是,无传感器解非常普遍且有用,主要是因为它们不依赖于传感器是否正常工作。它们通过使用一系列行动而无须任何感知,从未知初始位置正确定位零件。有时,即使存在可感知的条件规划,无传感器规划也会更好。
无传感器问题的解是一个动作序列,具体来说智能体是通过执行动作来在没有感知的情况下获得信息,通过不断执行动作来强迫世界到达某一个状态。与以往的算法不同的是,无观测信息的智能体是在信念状态空间而非物理状态空间中进行搜索,在信念状态空间中,问题是完全可观测的,因为智能体始终知道自己的信念状态。
信念状态问题与以往的搜索在问题形式化上也有所差异,主要表现在以下几点:
1、状态:信念状态空间包含物理状态的每一个可能子集。如果原问题$P$有$N$个状态,那么信念状态问题有$2^N$个信念状态,尽管有很多状态都无法从初始状态到达。
2、初始状态:通常,初始信念状态包含$P$中的所有状态,但是在许多情况下,智能体具有更多的先验知识。
3、动作:如果假定非法动作不会对环境产生影响,那么执行当前信念状态$b$下的任意物理状态的所有动作的并集都是安全的。如果非法动作可能导致严重后果,那么只允许执行动作的交集(对所有状态都合法的动作的集合)更安全。
4、转移模型:对于确定性动作,$b’$不会大于$b$,而对于非确定性动作,$b’$可能会大于$b$。
仍然存在问题:状态空间庞大,内存不够。
1、形式化紧凑表示;
2、避免使用标准搜索算法,进行增量信念状态搜索,每次为一个物理状态进行搜索,获得解后检测是否适用于其他状态,否则回溯寻找其他解。
部分可观测环境的搜索在问题形式化上与其他情况下搜索的最显著差异在于转移模型,该问题的转移模型分为三个阶段:
预测($prediction$)阶段:与无传感器问题相同,计算由动作所导致的信念状态,$Result(b, a)$。为了强调这是一个预测,将其记为$\hat{b} = Result(b, a)$,其中$b$上方的符号表示“估计值”,可以使用$Predict(b, a)$代替$Result(b, a)$。
可能感知($possible$ $percept$)阶段:计算在预测的信念状态下可以观测到的感知集合(用字母 o 表示观测到的感知):
$$
Possible-Percepts\left\{ o:o=percept\left( s \right) ,s\in \hat{b} \right\}
$$
更新($update$)阶段:为每个可能感知计算其可能得到的信念状态。更新后的信念状态$b_o$是$\hat{b} $中可能产生这一感知的状态集合:
$$
b_o=Updata\left( \hat{b},o \right) =\left\{ s:o=perpect\left( s,s\in \hat{b} \right) \right\}
$$
综上,转移模型被形式化定义为:
$$
\text{Re}sult\left( b,a \right) =\left\{ b_o:b_o=Updata\left( Predict\left( b,a \right) ,o \right) ,o\in Possible-Percepts\left( Predict\left( b,a \right) \right) \right\}
$$
一般来说,对于非确定性动作,$Predict$阶段信念状态增加,但是$Update$阶段信念状态又减少回去——只要感知提供了有用的识别信息。
使用如上的转移模型形式化,可以直接应用与或搜索算法得到问题的解,又由于是在信念状态问题中应用与或搜索算法,所以它返回的条件规划所测试的是信念状态,而非实际状态。
与标准搜索算法应用于无传感器问题的情况一样,与或搜索算法将信念状态看作和任何其他问题状态一样的黑盒。可以通过检查先前生成的信念状态——它们是当前状态的子集或超集——来改进这一点,就像求解无传感器问题一样。同样可以推导出与无传感器问题中描述的那些算法类似的增量搜索算法。与黑盒方法相比,它们提供了显著的加速。
部分可观测环境中的智能体先对问题形式化,接着调用搜索算法求解,然后执行解步骤。这种智能体和完全可
观测确定性环境中的智能体之间有两个主要区别。首先,问题的解将是一个条件规划而不是一个序列;为了执行$if$-$then$-$else$表达式,智能体需要测试$if$语句中的条件并执行正确的条件分支。其次,智能体需要在执行动作和接收感知时维护其信念状态。这一过程类似于式中的预测-观测-更新过程,但更加简单,因为感知是由环境给出的,而不是由智能体自己计算的。
在线搜索智能体和未知环境
此前的搜索算法主要关注使用离线搜索算法,它们在执行第一个动作之前就已经计算出一个完整的解。相比之下,在线搜索智能体则交替进行计算和动作:它首先执行一个动作,然后观测环境并计算下一个动作。在线搜索适用于动态或半动态环境,因为在这些环境中停止不动或计算时间太长都要付出代价。在线搜索在非确定性领域也很有用,因为它允许智能体将计算精力集中在实际发生的偶然事件上,而不是那些也许会发生但很可能不会发生的事件。
当然,这里需要权衡:智能体提前规划得越多,发现自己陷入困境的频率越低。在未知环境中,智能体不清楚存在什么状态或者动作会产生什么结果,必须使用自身的动作作为实验来了解环境。
通常,智能体的目标是以最小代价到达目标状态。(另一个可能目标是简单地探索整个环境。)代价是智能体在移动过程中产生的总的路径代价。通常将它与智能体事先知道搜索空间时所产生的路径代价(即已知环境中的最优路径)进行比较。在在线算法的术语中,这种比较被称为竞争比。
在线探索器很容易陷入死胡同:无法到达任何目标状态的状态。如果智能体不知道每个动作的后果,它可能会“跳进陷阱”,因此永远无法到达目标。一般来说,没有一种算法能在所有状态空间中都避免进入死胡同。
死胡同是机器人探索中的一个真正的难点许多地形中都存在从它发出某些动作不可逆的状态,之前提及的探索算法只保证在可安全探索的状态空间中是有效的,也就是说,从每个可达状态出发都存在可以到达的目标状态,所有动作都可逆的状态空间。
基础算法不适用于探索,因为会无路可走且无法随机重启,通常的做法是使用随机游走来探索环境。随机游走只是从当前状态中随机选择一个可用动作,可以优先考虑尚未尝试的动作。容易证明,当空间有限且可安全探索时,随机游走最终会找到一个目标或完成探索。但是,这一过程可能非常慢。
随机游走在无限的一维和二维网格上是完备的。在三维网格上,游走返回起点的概率只有大约 0.3405。
事实证明,增加爬山法的内存而非随机性是一种更有效的方法。基本思想是,存储从已访问的每个状态出发到达目标所需代价的“当前最佳估计”$H(s)$。$H(s)$开始时只是启发式估计,然后根据智能体在状态空间中获得的经验不断更新。实现这一算法的智能体称为实时学习 A*($LRTA^*$)智能体,它用$result$表构建环境地图。它首先更新刚刚离开的状态的代价估计值,然后根据当前的代价估计值选择“显然最佳”移动。一个重要的细节是,在状态$s$下尚未尝试的动作总是被假定为以最少的可能代价,即$h(s)$直接到达目标。这种不确定性下的乐观主义鼓励智能体去探索新的、可能更有希望的路径。
$LRTA^*$智能体保证在任何有限的、可安全探索的环境中都能找到目标。然而,不同于$A^*$,$LRTA^*$在无限状态空间中是不完备的——在某些情况下,它可能被无限地引入歧途。在最坏情况下,探索状态数为$n$的环境可能需要$O(n^2)$步,但通常情况下会比这种情况好得多。