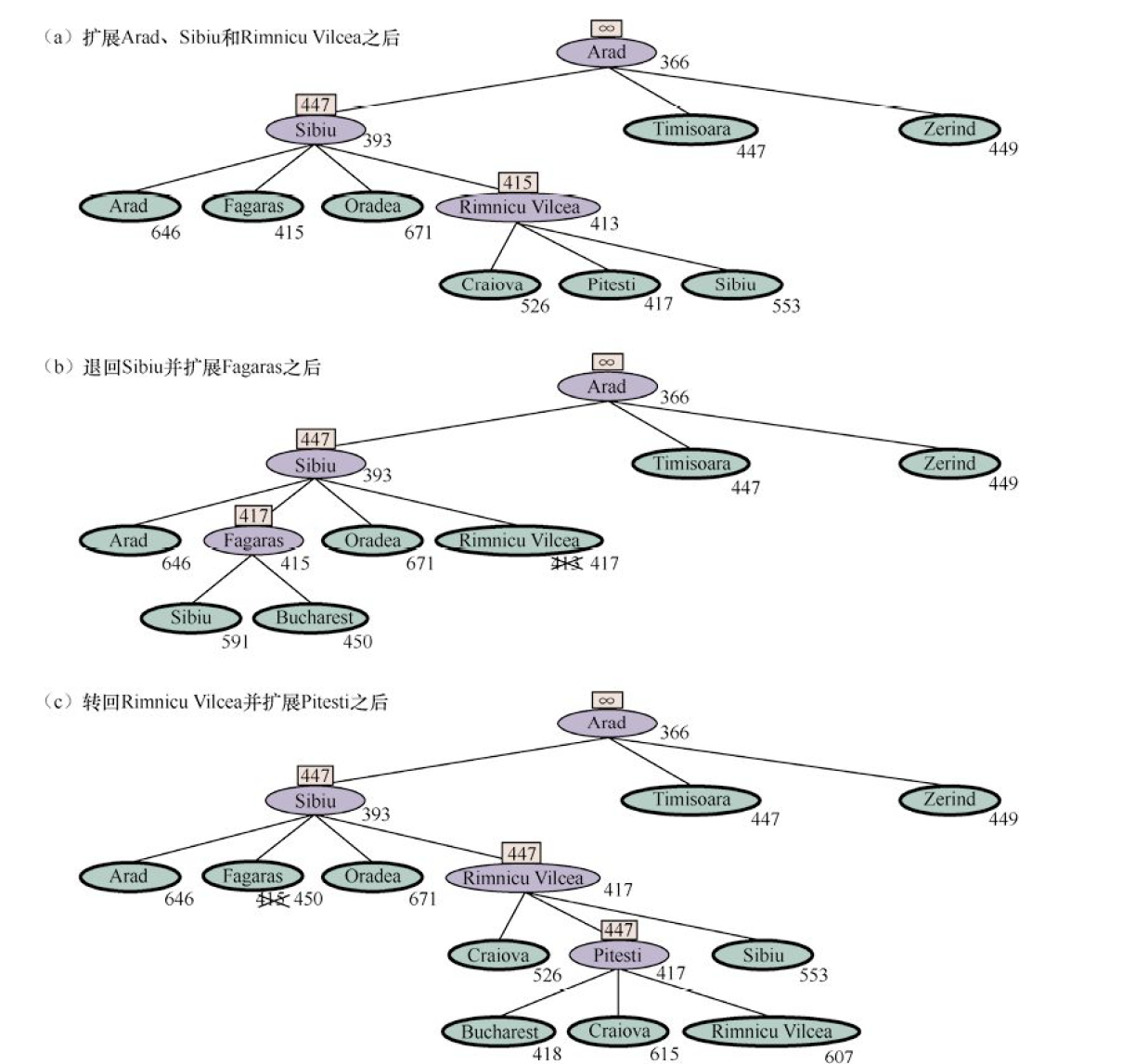
满意搜索
$A^*$搜索有很多好的性质,但它扩展了大量节点。如果愿意接受次优但“足够好”的解——即满意解,则可以探索更少的节点(花费更少的时间和空间)。
如果允许$A^*$搜索使用不可容许的启发式函数,那么算法就有可能错过最优解,但是可能更准确,从而减少了需要扩展的节点数。
例如,道路工程师知道弯道指数的概念,它是应用于直线距离的乘数,用来说明道路的典型曲率。弯道指数 1.3 意味着如果两个城市的直线距离相距 10 千米,那么它们之间的最优路径的一个恰当的估计值是 13 千米。
将这一思想应用于任何问题,即采用一种称为加权$A^*$搜索的方法,对启发式函数的值进行更重的加权,评价函数为:
$$
f\left( n \right) =g\left( n \right) +W\cdot h\left( n \right)
$$
加权$A^*$搜索总搜索到一个代价稍高的解,但搜索时间要快得多。加权搜索使得已达状态的等值线专注于趋向某个目标。这意味着需要探索的状态变少,但如果最优路径偏离加权搜索的等值线,则无法找到最优路径。
一般来说,如果最优解的代价是$C^*$,那么加权$A^*$搜索将找到一个代价介于$C^*$和$W\cdot C^*$之间的解;但在实践中,通常结果更接近于$C^*$而不是$W\cdot C^*$。
内存受限搜索
$A^*$搜索的主要问题是它对内存的使用较多,因此需要一些方法来节省内存,三个有助于节省内存的方法包括:
- $A^*$搜索的内存需要同时维护$frontier$表和$resched$表的信息,可以通过较为复杂的算法在只维护一个信息的情况下进行搜索,但是这样会导致时间复杂度的提升。
- 当可以证明不再需要某些状态时,就将它们从$reached$中删除。可以利用分离性质,同时禁止掉头行动,以确保所有行动要么是从边界向外移动,要么是移动到另一个边界状态。在这种情况下,只需检查边界就能判断是否有冗余路径,并且可以删除$reached$状态表。
- 维护引用计数——到达某一状态的次数,并且在再也没有路径可以到达该状态时将其从$reached$表中删除。
束搜索对边界的大小进行了限制,最简单的方法是只保留具有最优$f$值的$k$个节点,放弃其他已扩展节点。这显然会导致搜索变成不完备的和次优的算法,但可以通过选取合适的$k$以充分利用可用内存,算法执行速度也会更快,因为它只扩展了较少的节点。对于许多问题,它可以找到很好的近似最优解。
另一种形式的束搜索并不严格限制边界的大小,而是保留$f$值在最优$f$值的某邻域内的所有节点。这样的话,当存在几个强得分节点时,只会保留几个节点,但如果不存在强节点,则会保留更多节点,直到出现一个强节点。
迭代加深$A^*$搜索与$A^*$搜索的关系就像是迭代加深搜索和深度优先搜索的关系一样。$IDA^*$既拥有$A^*$的优点,又不要求在内存中保留所有已达状态,这样做的代价是需要多次访问某些状态。它是一种非常重要且常用的用于解决内存不足问题的算法。
在标准的迭代加深搜索中,截断值为深度,每次迭代深度增加 1。而在$IDA^*$中,截断值是$f$代价$(g+h)$;在每次迭代中,新的截断值为超过上一次迭代截断值的节点中最小的$f$代价。换句话说,每次迭代都会彻底地搜索一个$f$等值线,找到一个刚好超出该等值线的节点,并使用该节点的$f$代价作为下一个等值线。
递归最佳优先搜索试图模拟标准的最佳优先搜索的操作,但仅仅使用线性空间。RBFS 类似于递归深度优先搜索,但它不是沿着当前路径无限地向下搜索,而是使用$f$_$limit$变量跟踪从当前节点的任意祖先节点可得到的最优备选路径的$f$值。
如果当前节点超过了这个限制,那么递归将回到备选路径上,并原将路径上每个节点的$f$值替换为一个倒推值其子节点的最优$f$值。通过这种方式,$RBFS$可以记住被它遗忘的子树中最优叶节点的$f$值,因此,在之后的某个时刻,$RBFS$可以决定是否要重新扩展该子树。
如果启发式函数$h(n)$是可容许的,那么$RBFS$是最优的。它的空间复杂性在最深的最优解的深度上是线性的,但时间复杂性很难刻画:既取决于启发式函数的准确性,也取决于最优路径随节点扩展变化的频率。它按照$f$得分递增的顺序来扩展节点,即使$f$是非单调的。
$SMA^*$很像$A^*$算法,不断扩展最优叶节点,直到内存被填满。此时,它不能再为搜索树添加新节点,除非删除旧节点。$SMA^*$总是丢弃最差的叶节点,即$f$值最大的叶节点。如果所有叶节点的$f$值都相同,为了避免算法选择同一个节点进行删除和扩展操作,$SMA^*$扩展最新的最优叶节点并删除最老的最差叶节点。
当只有一个叶节点时,这两者是同一个节点,但在这种情况下,当前的搜索树一定是一条从根节点到叶节点的占满所有内存的单一路径。如果叶节点不是目标节点,那么即使它在最优解路径上,也无法在可用内存范围内得到这个解。
和$RBFS$一样,$SMA^*$将被遗忘节点的值备份到其父节点。这样,被遗忘子树的祖先知道该子树中最优路径的质量。有了这一信息,只有在所有其他路径看起来都比它已经遗忘的路径更差时,$SMA^*$才会重新生成该子树。这意味着如果节点 n 的所有后代都被遗忘了,那么尽管算法不知道从$n$开始应该走哪条路径,但仍知道是否应该从$n$开始走。
如果存在任意可达解,也就是说,如果最浅的目标节点的深度$d$小于内存大小(用节点数表示),那么$SMA^*$就是完备的。如果存在可达的最优解,那么$SMA^*$就是最优的;否则,就返回当前最优的可达解。在实践中,$SMA^*$是寻找最优解的一个相当稳健的选择,特别是当状态空间是一个图、行动代价不一致,并且生成节点的总开销相比维护边界集和已达集的总开销更大时。
然而,在非常困难的问题上,常常会出现$SMA^*$被迫在许多候选解路径之间来回不断切换的情况,只有一小部分路径可以存入内存。那么,重复生成相同节点就需要额外的时间,这意味着,在给定无限内存的情况下可以用$A^*$实际求解的问题,对于$SMA^*$将变得难以处理。也就是说,从计算时间的角度,内存限制会使问题变得难以处理。虽然还没有现有理论解释如何在时间和内存之间权衡,但这似乎是一个不可避免的问题。唯一的出路是放弃最优性要求。
双向启发式搜索
当启发式函数很好的时候,双向启发式搜索的增益并不大;当启发式函数一般时,双向搜索的增益最优。使用$f_2$评价函数和可容许的启发式函数$h$的双向搜索算法是完备且最优的。
$$
f_2\left( n \right) =\max \left( 2g\left( n \right) ,g\left( n \right) +h\left( n \right) \right)
$$