有信息搜索($informed$ $search$)策略——使用关于目标位置的线索——通常比无信息搜索策略更有效地找到解。线索以启发式函数($heuristic$ $function$)的形式出现,记为 h(n):
贪心算法  ($greedy$ $best$-$first$ $search$)
($greedy$ $best$-$first$ $search$)
贪心最佳优先搜索首先扩展$h(n)$值最小的节点——看起来最接近目标的节点——因为这样可能可以更快找到解。因此,评价函数$f(n) =h(n)$。在每次迭代中,贪心最佳优先搜索都会做出在当前看来最优的(即可以最接近目标的)选择,但这也会导致贪心法在全局意义上可能产生比谨慎的算法更糟糕的结果。
贪心最佳优先图搜索在有限状态空间中是完备的,但在无限状态空间中是不完备的。最坏情况下的时间复杂性和空间复杂性是$O\left( \left| V \right| \right) $。然而,使用一个好的启发式函数,复杂性可以大大降低,对于某些问题可以达到$O(bm)$。
$A^*$搜索($A$ $star$ $Search$)
$A^*$搜索的评价函数是:
$$
f\left( n \right) =g\left( n \right) +h\left( n \right)
$$
其中,$g\left( n \right)$是从初始状态到节点$n$状态的花费值,$h\left( n \right)$从节点$n$到一个目标状态的最短路径的代价估计值。
$A^*$搜索是完备的。它的代价最优性取决于启发式函数的某些性质。关键性质是可容许性($admissibility$):一个可容许的启发式函数永远不会高估到达某个目标的代价。(因此,一个可容许的启发式函数是乐观的。)
$Proof$(反证法):
假设实际上的最优解是$C^*$,算法返回的是次优解$C$,故在最优路径上存在一点$n$,使得返回路径在$n$的前驱状态时未扩展节点$n$,易知此时有:
$$
f\left( n \right) =g\left( n \right) +h\left( n \right) >C^*
$$
使用符号$g^*(n)$表示从起点到$n$的最优路径的代价,$h^*(n)$表示从$n$到最近目标的最优路径的代价。由于节点$n$在最佳路径上,又由可容许性有:
$$
f\left( n \right) =g^*\left( n \right) +h\left( n \right) \le g^*\left( n \right) +h^*\left( n \right) =C^*
$$
综上,$f\left( n \right) \le C^*$与$f\left( n \right) >C^*$相互矛盾,故得证!
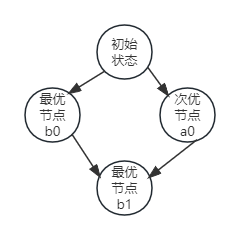
先说明为什么在可容许的情况下图$A^*$搜索不是最优的,假设最优路径上任意两点之间都是一致的,而其他节点都是不一致的,故可考虑这样一种情况:
故在扩展某初始状态$n$时有:
$$
f\left( b_0 \right) =g\left( b_0 \right) +h\left( b_0 \right) =g\left( n \right) +c\left( n,a,b_0 \right) +h\left( b_0 \right)
$$
$$
\ge g\left( n \right) +h\left( n \right) =f\left( n \right)
$$
$$
f\left( a_0 \right) =g\left( a_0 \right) +h\left( a_0 \right) =g\left( n \right) +c\left( n,a,a_0 \right) +h\left( a_0 \right)
$$
$$
< g\left( n \right) +h\left( n \right) =f\left( n \right)
$$
故$f\left( b_0 \right) >f\left( a_0 \right) $,此时易知从$a_0$扩展$b_1$时的$f\left( b_1 \right) < f\left( b_0 \right) $故节点$b_1$先于$b_0$被扩展。由于此为图搜索,故节点$b_1$不会被再次扩展,此时图$A^*$搜索此时不具代价最优性。
接下来证明在一致性条件下,图$A^*$搜索的代价最优性:
$Proof:$首先证明:$f(n)$在任何路径上都是非递减的,设$n’$为$n$的后继节点,故有:
$$
f\left( n’ \right) =g\left( n’ \right) +h\left( n’ \right) =g\left( n \right) +c\left( n,a,n’ \right) +h\left( n’ \right)
$$
$$
\ge g\left( n \right) +h\left( n \right) =f\left( n \right)
$$
再证明当扩展节点$n$时,已经找到到达节点$n$的最优路径。易知,$f(n)$大于任意前驱节点$n’$,故节点$n$被扩展时所有能够到达$n$的路径均已被探索。
综上,可证图$A^*$搜索在一致性条件下有代价最优性。
$Proof:$首先证明:初始节点$n_0$满足可容许性,$n_0$沿任意路径$n_0,n_1,n_2,…,n_s$进行扩展,由于一致性有:
$$
h\left( n_0 \right) \le c\left( n_0,a_0,n_1 \right) +h\left( n_1 \right) \le \sum_{i=0}^{s-1}{c\left( n_i,a_i,n_{i+1} \right)}=g\left( n_s \right) =h^*\left( n_0 \right)
$$
再证节点$n_k$满足可采纳性:
$$
h\left( n_k \right) \le h\left( n_{k+1} \right) +c\left( n_k,a_k,n_{k+1} \right) \le \sum_{i=k}^{s-1}{c\left( n_i,a_i,n_{i+1} \right)}=g\left( n_s \right) -g\left( n_k \right) =h^*\left( n_k \right)
$$
$A^*$搜索的时间复杂度是$O(b^{\epsilon d})$,其中$\epsilon = (h^* – h)/h^*$,空间复杂度为$O(b^d)$。具有一致启发式函数的$A^*$搜索是效率最优的,$A^*$之所以高效,是因为它会对那些对于寻找最优解没有帮助的搜索树节点进行剪枝($pruning$),即使它们是根的子节点并且是采用一致代价搜索或广度优先搜索时首先扩展的节点,它们也永远不会被$A^*$搜索扩展,对许多人工智能领域来说,剪枝(不必进行检查就可以排除不正确的答案)非常重要。