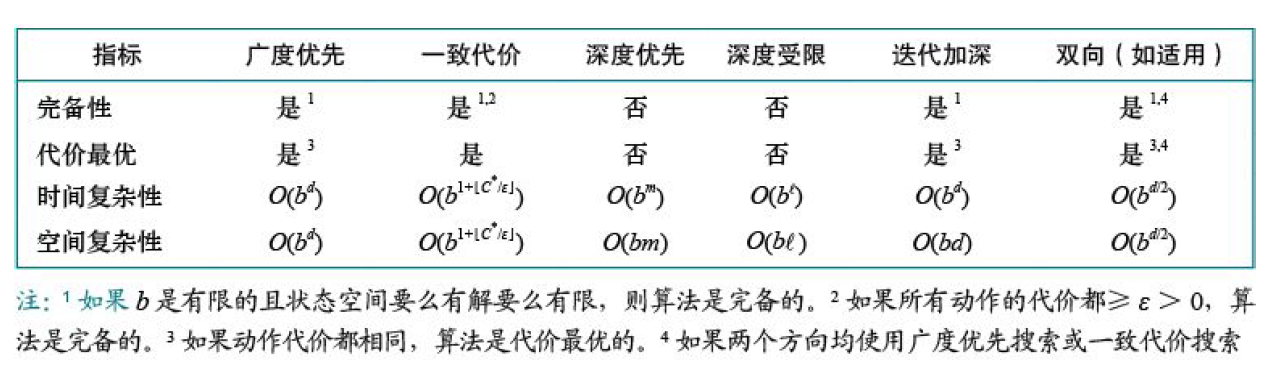
无信息搜索算法是指在不提供有关某个状态与目标状态的接近程度的任何线索的情况下进行的搜索。
广度优先搜索($BFS$,$breadth$-$first$ $search$)
当所有动作的代价相同时,正确的策略是采用广度优先搜索,即先扩展根节点,然后扩展根节点的所有后继节点,再扩展后继节点的后继,以此类推。
这是一种系统的搜索策略,因此即使在无限状态空间上也是完备的。最简单的实现方法是通过调用$Best$-$First$-$Search$来实现,将评价函数$f(n)$设置为节点的深度,即到达该节点所需的动作数。
先进先出队列比优先队列速度更快,并且能提供正确的节点顺序;
在$BSF$中搜索第一次到达某个状态,就已经是最小花费了。这意味着$BFS$可以进行早期目标测试,即在生成节点后立即检查该节点是否为一个解。
$BFS$相当于在搜索一棵均衡树,其中每个状态都有$b$个后继。搜索树的根生成$b$个节点,每个节点又生成$b$个节点,第二层总共是$b^2$个节点。每个节点又生成$b$个节点,从而在第三层产生$b^3$个节点,以此类推。现在假设解的深度为$d$,那么生成的节点总数为:
$$
1+b+b^2+\cdot \cdot \cdot +b^d=O\left( b^d \right)
$$
所有节点都存储在内存中,所以时间复杂性和空间复杂性都是$O(b^d)$。这样的指数级上界是可怕的,对广度优先搜索来说,内存需求是一个比执行时间更严重的问题,但时间仍然是一个重要因素。一般来说,除了最小的问题实例,指数级复杂性的搜索问题无法通过无信息搜索求解。
Dijkstra 算法或一致代价搜索($uniform$-$cost$-$search$)
一致代价搜索算法的思想是在路径代价一致的边缘中展开。该算法可以通过调用$Best$-$First$-$Search$,设置评价函数为$Path$-$Cost$来实现。一致代价搜索采用后目标检测的方法,即只在扩展节点时测试其是否为目标节点,而不是在生成节点时测试,因为生成节点时并不能判断这是最优的路径。
一致代价搜索的复杂性用$C^*$和$\epsilon $表示,$C^*$是最优解的代价,$\epsilon $是每个动作代价的下界,$\epsilon >0$。那么算法在最坏情况下的时间复杂性和空间复杂性是$O\left( b^{1+\lfloor C^*/\epsilon \rfloor} \right) $,比$b^d$大得多。这是因为一致代价搜索在探索包含一个可能有用的高代价动作的路径之前,可能会先探索具有低代价动作的大型树。当所有动作代价相同时,$b^{1+\lfloor C^*/\epsilon \rfloor}$等于$b^{d+1}$,这时一致代价搜索类似于广度优先搜索。
一致代价搜索是完备的,也是代价最优的,因为它找到的第一个解的代价至少与边界上的任何其他节点的代价一样小。一致代价搜索会按照代价递增的顺序系统地考虑所有路径,而不会陷入一直沿单一无限路径探索的困境(假设所有动作的代价$\epsilon >0$)。
深度优先搜索($DFS$,$depth$-$first$ $search$)
深度优先搜索总是优先扩展边界中最深的节点。它可以通过调用$Best$-$First$-$Search$来实现,其中评价函数$f$为深度的负数。然而,它通常不是以图搜索的形式实现而是以树状搜索(不维护已达状态表)的形式实现。
$DFS$先直接到达搜索树的最深层,这里的节点不存在后继节点。然后,搜索将“回退”到下一个仍存在未扩展后继节点的最深的节点。深度优先搜索不是代价最优的,它会返回它找到的第一个解,即使这个解不是路径代价最小的。
对于树型的有限状态空间,算法是有效且完备的。对于无环状态空间,算法可能会通过不同路径多次扩展同一状态,但是(最终)将系统地探索整个空间。在有环状态空间中,深度优先搜索算法可能陷入无限循环;因此,一些深度优先搜索算法的实现会检查每个新节点是否存在循环。在无限状态空间中,深度优先搜索不是系统性的:即使没有循环,它也可能陷入无限路径。因此,深度优先搜索是不完备的。
深度优先搜索对内存的需求要小得多。深度优先搜索根本不保留$reached$表,并且边界集很小:如果将广度优先搜索中的边界集视为不断扩展的球体的表面,那么深度优先搜索中的边界集只是球体的半径。
对于有限树状状态空间,深度优先的树状搜索所花费的时间与状态数成正比,其空间复杂性仅为$O(bm)$,其中$b$是分支因子,$m$是树的最大深度。有些问题在广度优先搜索时需要$EB$量级的内存,而在深度优先搜索时仅需要$KB$量级。
回溯搜索使用的内存更少,在回溯搜索中,一次只生成一个后继,而不是所有后继节点;每个部分扩展的节点会记住下一个要生成的后继节点。此外,回溯通过直接修改当前状态描述而不是为一个全新的状态分配内存来生成后继状态。这将内存需求减少到只有一个
状态描述和一条具有$O(m)$个动作的路径;与深度优先搜索的$O(bm)$个状态相比,节省了大量资源。
通过回溯可以为当前路径上的状态维护一个有效的集合数据结构,从而使检查循环的时间从$O(m)$减少到$O(1)$。为了使回溯起作用,必须能够在回溯时撤销每个动作。
深度受限搜索($depth$-$limited$ $search$)与迭代加深搜索($iterative$ $deepening$ $search$)
深度受限搜索被用于避免深度优先搜索陷入无限路径,这是一个深度优先搜索的改进版本,在深度受限搜索中,通过设置深度界限$\ell $,将深度$\ell $上的所有节点视为不存在后继节点。深度受限搜索算法的时间复杂性为$O(b)$,空间复杂性为$O(b)$。如果对$\ell $的选择不当,算法将无法得到解,成为不完备的算法。
由于深度优先搜索是一种树状搜索,通常无法避免在冗余路径上浪费时间,但可以以一定的计算时间为代价来消除循环。沿着父节点向上查看几个节点,就能检测出大多数循环;更长的循环则由深度界限处理。
迭代加深搜索解决了如何选择一个合适的$\ell $的问题,方法是尝试所有值:首先是$0$,然后是$1$,然后是$2$,依次类推——直到找到一个解,或者深度受限搜索返回$failure$值。
迭代加深搜索结合了深度优先和广度优先搜索的许多优点。和深度优先搜索一样,它对内存的需求也不大:当问题存在解时,是$O(bd)$,在不存在解的有限状态空间上,是$O(bm)$。与广度优先搜索一样,迭代加深搜索对于所有动作都具有相同代价的问题是最优的,并且在有限无环状态空间上是完备的,或者说在任何有限状态空间上,当检查路径节点上所有的循环时,它都是完备的。
存在解时,时间复杂性为$O(b^d)$,不存在解时,时间复杂性为$O(b^m)$。与广度优先搜索相同,迭代加深搜索的每次迭代也会生成一个新层级,但是广度优先搜索将所有节点都存储在内存中,而迭代加深搜索则会重复之前的层级,从而以花费更多的时间为代价节省了内存。
迭代加深搜索可能看起来很浪费,因为搜索树顶端附近的状态被多次重复生成。但是对于许多状态空间,大多数节点位于底层,所以上层是否重复并不重要。在迭代加深搜索中,底层(深度$d$)的节点被生成一次,倒数第二层的节点被生成两次,以此类推,直到根节点的子节点(生成$d$次)。所以在最坏情况下生成的节点总数是
$$
\left( d \right) b^1+\left( d-1 \right) b^2+\left( d-2 \right) b^3\cdot \cdot \cdot +b^d=O\left( b^d \right)
$$
实际上和$BFS$在同一个数量级,当然还有更好的一个方法就是:先运行广度优先搜索,直到几乎消耗掉所有可用内存,然后对边界集中的所有节点应用迭代加深搜索。通常,当搜索状态空间大于内存容量而且解的深度未知时,迭代加深搜索是首选的无信息搜索方法。
双向搜索($bidirectional$ $search$)
双向搜索同时从初始状态正向搜索和从目标状态反向搜索,直到这两个搜索相遇。算法的动机是$b^{d/2}+b^{d/2}$要比$b^d$小得多。为此,算法需要维护两个边界集和两个已达状态表,并且要能反向推理:如果状态$s’$是$s$的正向后继,那么$s$就是$s’$的反向后继。当两个边界触碰到一起时,算法就找到了一个解。
双向搜索有很多不同版本,就像有很多不同的单向搜索算法一样。通常的作法是双向最佳优先搜索。尽管存在两个独立的边界,但要扩展的节点始终是两个边界中的评价函数值最小的节点。事实上,算法找到的第一个解不一定是代价最优的解,能否得到代价最优解由控制算法结束的函数决定。