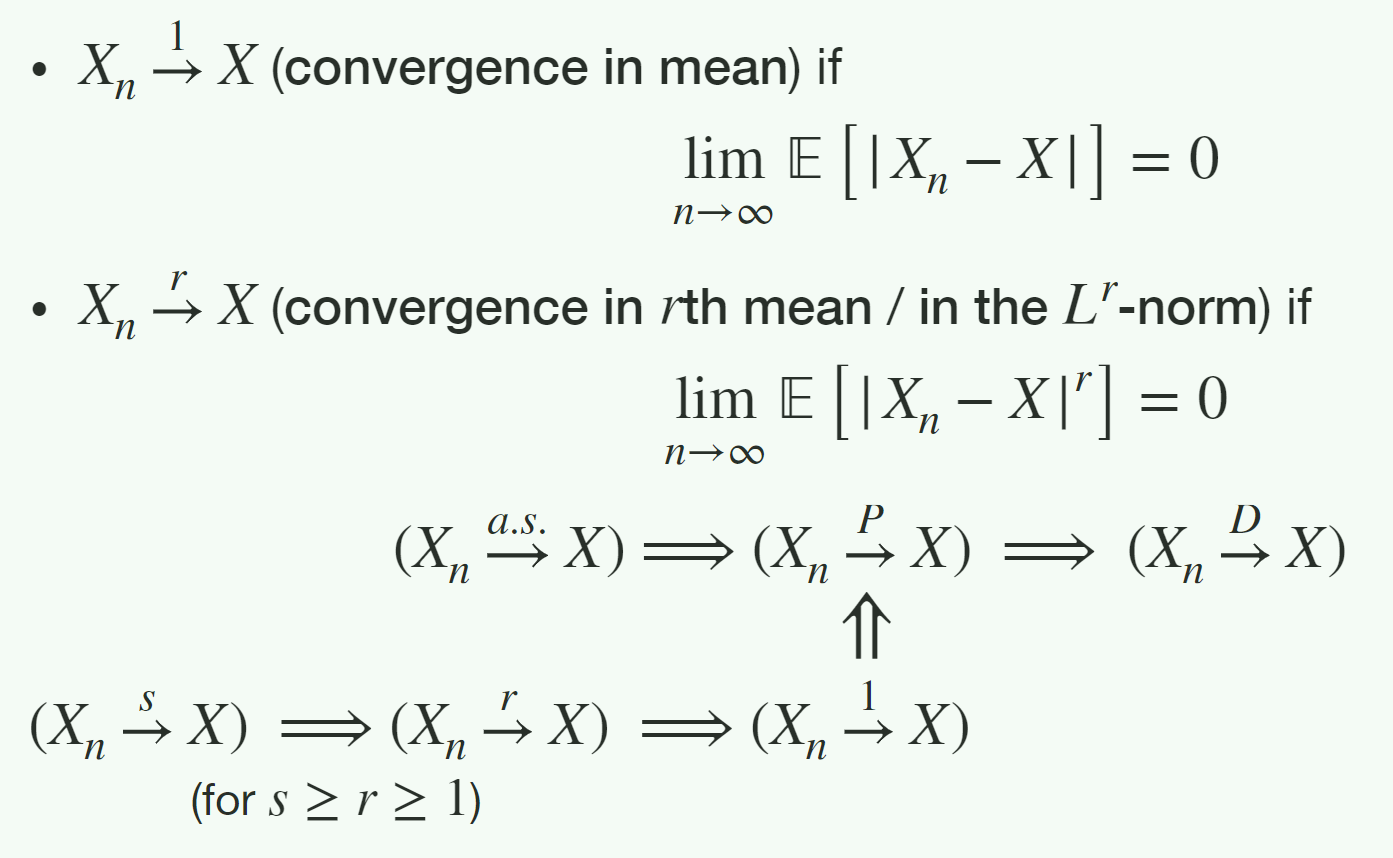继续探讨收敛模式
几乎必定收敛的条件
几乎必定收敛 $VS$ 依概率收敛
延伸
耦合
Skorokhod 定理：对于一个概率空间$(X,\mathscr{F},\mu)$中的依分布收敛的随机变量列$f_n\overset{d}\rightarrow f$，总是存在另一个概率空间 $(\tilde{X},\tilde{\mathscr{F}},\tilde{\mu})$中的随机变量列$\tilde{f_n}\overset{d}=f_n,\tilde{f}\overset{d}=f$，使得$\tilde{f_n}\overset{a.s.}\rightarrow\tilde{f}$。从依分布收敛变换到几乎必然收敛所要付出的代价更加大，我们需要把整个概率空间都换掉！PPT 的证明运用了逆变换采样：
连续映射定理
其他收敛模式
