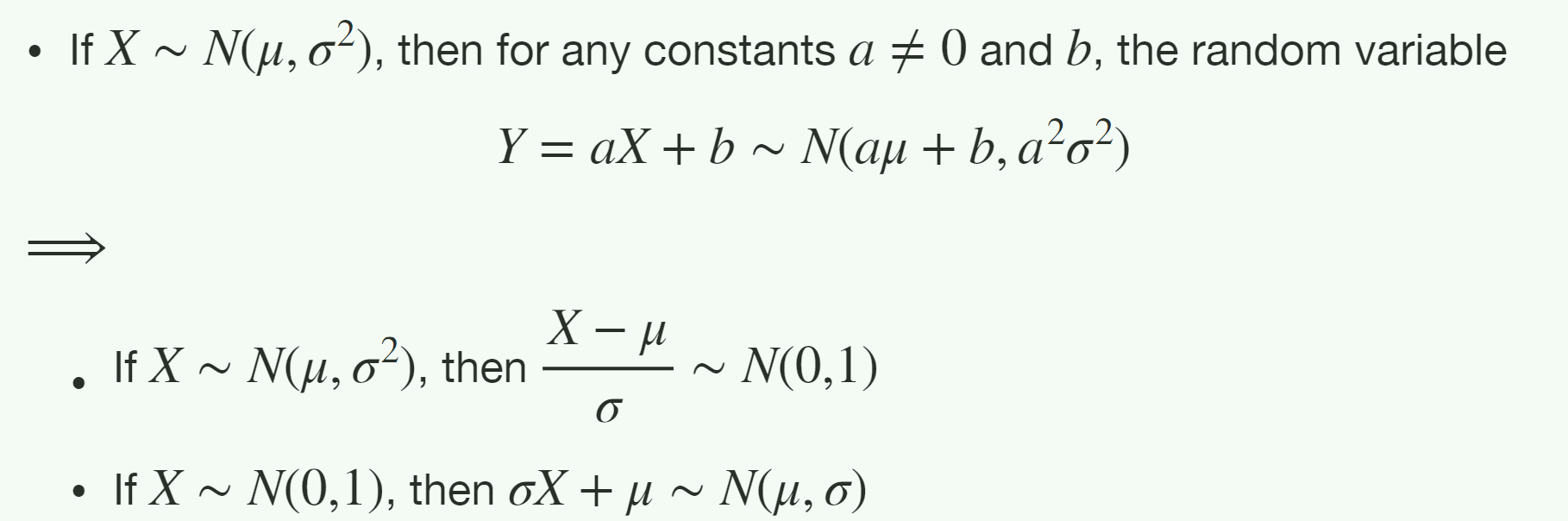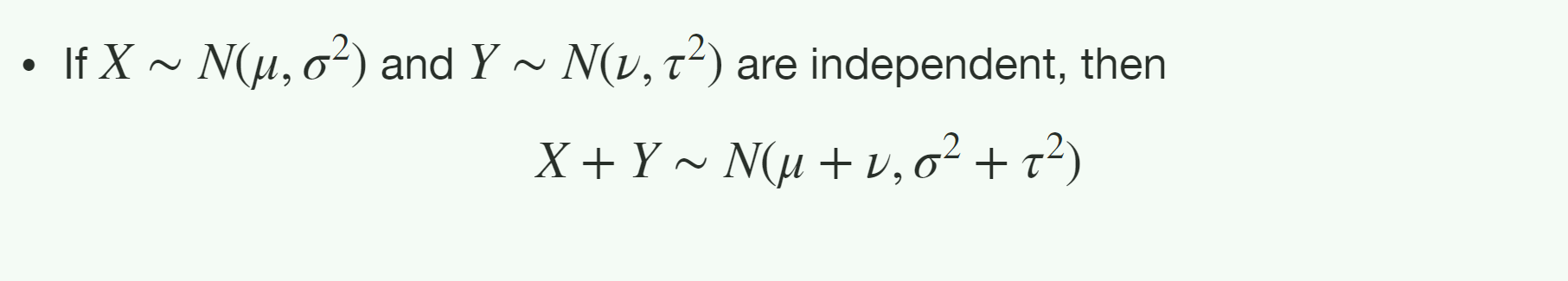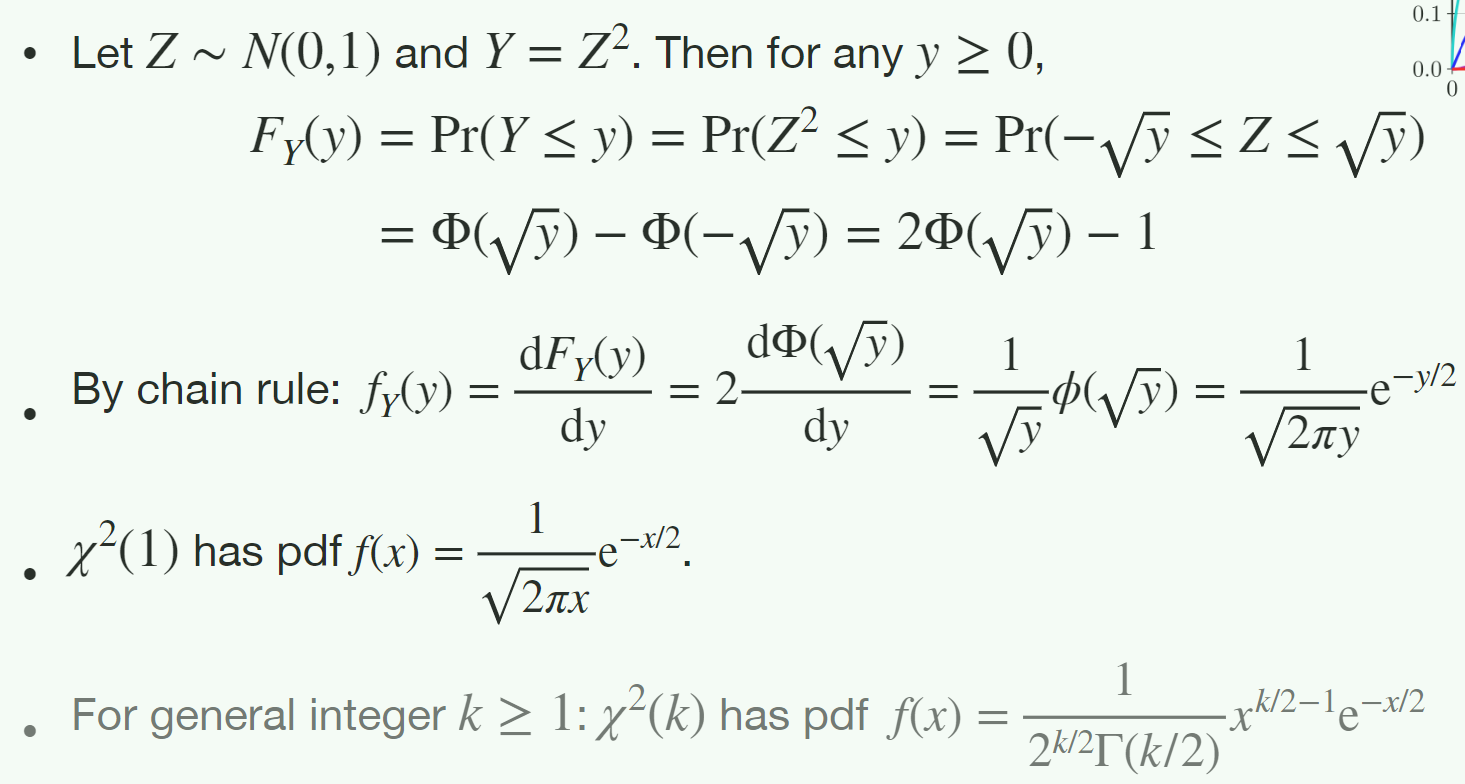引入
正态分布
一些性质
线性变换
卷积
线性变换的卷积证明
标准正态分布
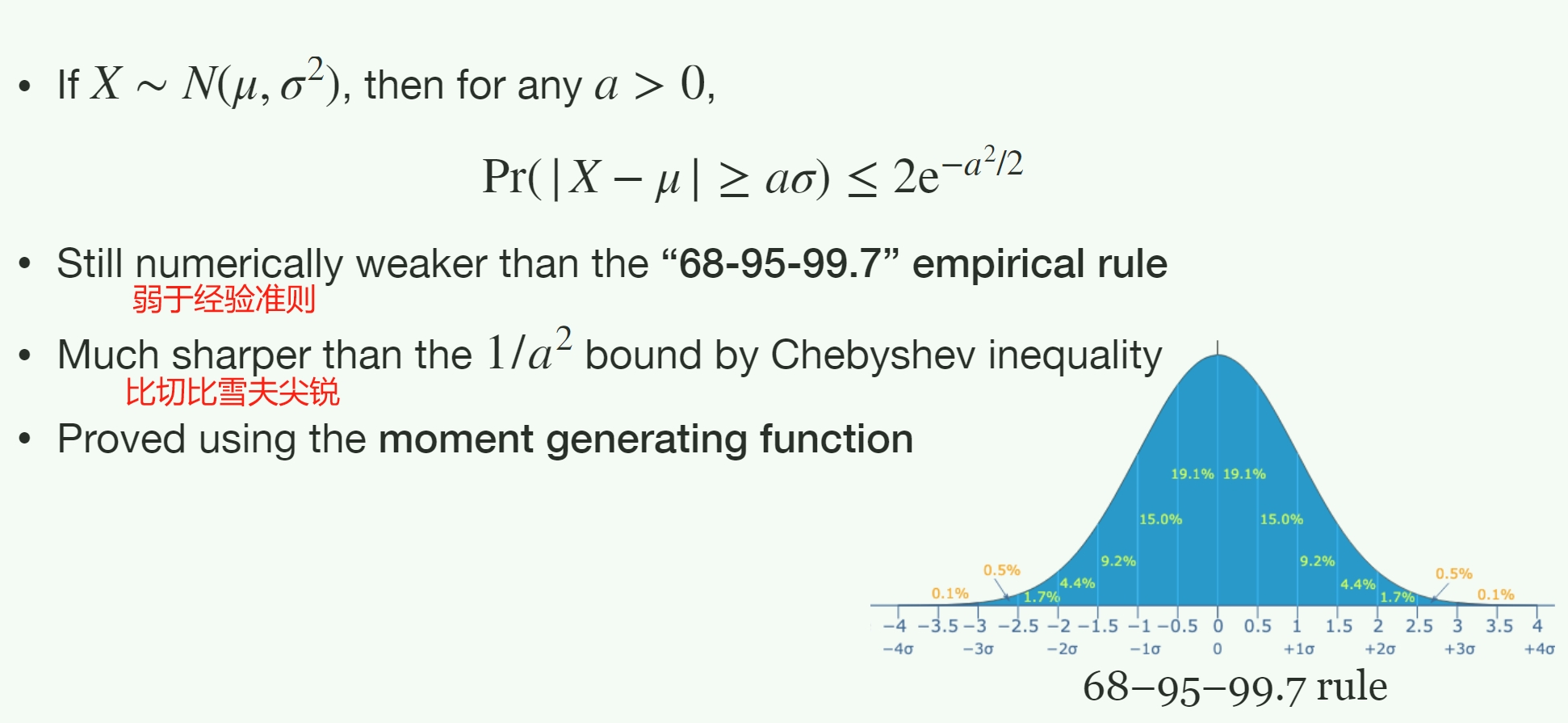
Large Deviation (Concentration) Bound
引入
矩母函数与标准正态分布的矩母函数
引入矩母函数后的再探讨
衍生分布
二元正态分布
已知二元正态分布服从$\mathscr{N}~\left( \mu _1,\mu _2,\sigma _{1}^{2},\sigma _{2}^{2},\rho \right) $则$aX+bY+c$服从一元正态分布：
$$
\mathscr{N}~\left( a\mu _1+b\mu _2+c,a^2\sigma _{1}^{2}+b^2\sigma _{2}^{2}+2ab\rho \sigma _1\sigma _2 \right)
$$
在 2023 年的真题中，已知$X，Y$服从二维正态分布$\mathscr{N}~\left( 1,-2,4,9,1/4 \right) $，求解马尔可夫不等式$Pr(|2X+Y|^2≥1)≤$？易知本题只需要求$\mathbb{E}\left[ \left| 2X+Y \right|^2 \right] $，显然有：
$$
\mathbb{E}\left[ \left| 2X+Y \right|^2 \right] =\mathbb{E}\left[ \left( 2X+Y \right) ^2 \right] =Var\left( 2X+Y \right) +\mathbb{E}\left[ 2X+Y \right] ^2
$$
通过简单计算可得：
$$
Var\left( 2X+Y \right) =a^2\sigma _{1}^{2}+b^2\sigma _{2}^{2}+2ab\rho \sigma _1\sigma _2=31
$$
$$
\mathbb{E}\left[ 2X+Y \right] ^2=0
$$
原题得解！
多元正态分布
卡方分布
