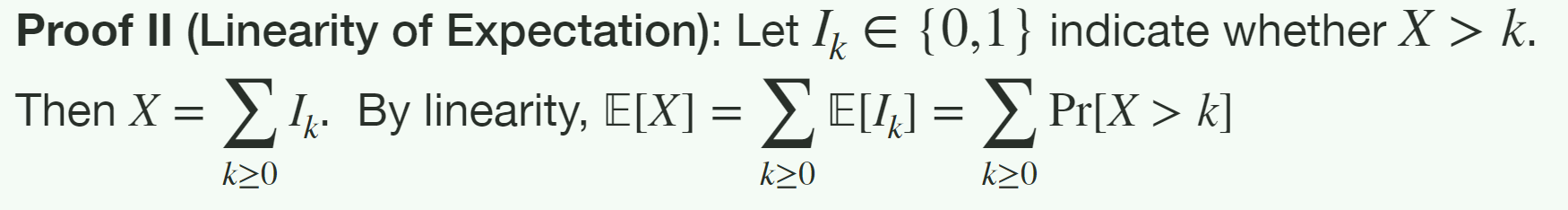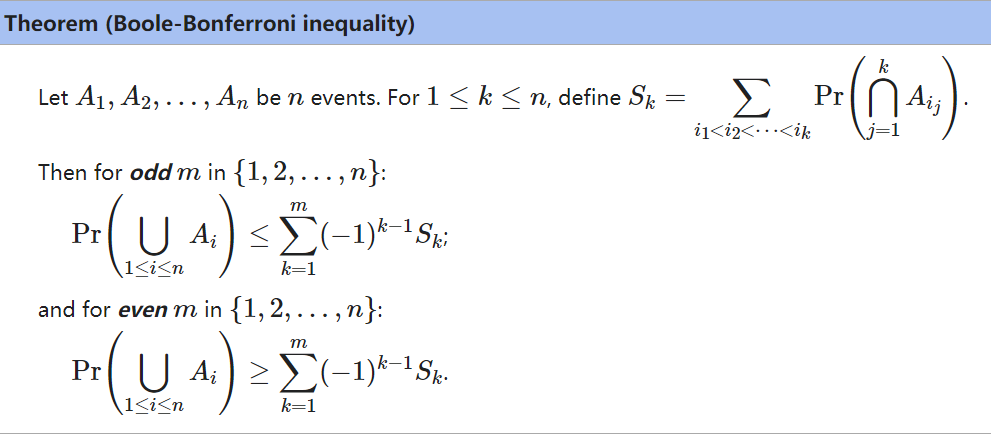855学习记录之概率论随机变量（2）期望的线性—— 炎泽汐$de$ Blog

文章目录[隐藏]

期望的线性基础
补充

期望的线性基础

负二项分布的期望

模式匹配

优惠券收集

非负随机变量的期望非负性

$Proof1$：

$$
\mathbb{E}\left[ X \right] =\sum_{x\ge 0}{x\cdot Pr\left( X=x \right) =\sum_{x\ge 0}{\sum_{k=0}^{x-1}{Pr\left( X=x \right)}=\sum_{k\ge 0}{Pr\left( X>k \right)}}}
$$

补充

Principle of Inclusion-Exclusion

令$I(A) \in \left\{ 0,1 \right\} $是事件$A$的指标随机变量，易得：

$$
\bigstar I\left( A^c \right) =1-I\left( A \right)
$$

$$
\clubsuit I\left( A\cap B \right) =I\left( A \right) \cdot I\left( B \right)
$$

对于事件序列$A_1,A_2,…,A_n$有：

$$
I\left( \bigcup_{i=1}^n{A_i} \right) \xlongequal{\bigstar}1-I\left( \left( \bigcup_{i=1}^n{A_i} \right) ^c \right) =1-I\left( \bigcap_{i=1}^n{A_{i}^{c}} \right)
$$

$$
\xlongequal{\clubsuit}1-\prod_{i=1}^n{I\left( A_{i}^{c} \right)}\xlongequal{\bigstar}1-\prod_{i=1}^n{\left( 1-I\left( A_i \right) \right)}
$$

$$
=1-\sum_{S\subseteq \left\{ 1,2,…n \right\}}{\left( -1 \right) ^{\left| S \right|}\cdot \prod_{I\in S}{I\left( A_i \right)}}
$$

$$
\xlongequal{\clubsuit}\sum_{\oslash \ne S\subseteq \left\{ 1,2,…n \right\}}{\left( -1 \right) ^{\left| S \right|-1}\cdot I\left( \bigcap_{i\in S}{A_i} \right)}
$$

根据期望的线性法则有：

$$
\mathbb{E}\left( I\left( \bigcup_{i=1}^n{A_i} \right) \right) =Pr\left( \bigcup_{i=1}^n{A_i} \right) =\xlongequal{\clubsuit}\sum_{\oslash \ne S\subseteq \left\{ 1,2,…n \right\}}{\left( -1 \right) ^{\left| S \right|-1}\cdot Pr\left( \bigcap_{i\in S}{A_i} \right)}
$$

Boole-Bonferroni Inequality