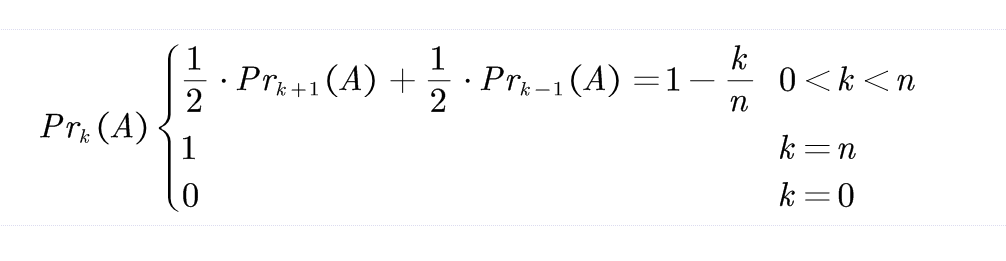全概率公式
$Proof$：1、令互不相交事件序列$B_1,B_2,…B_n$构成样本空间，且对于任意$i$都有$Pr(i) \ge 0$；
2、则事件序列$A\cap B_1,\cap B_2,…A\cap B_n$亦不相交，且$A=\bigcup_{i=1}^n{A\cap B_i}$；
3、故$Pr\left( A \right) =\sum_{i=1}^n{Pr\left( A\cap B_i \right)}$；
4、更进一步有$Pr\left( A \right) =\sum_{i=1}^n{Pr\left( A|B_i \right) \cdot Pr\left( B_i \right)}$。
还是经典的三门问题，定义事件$A$为赢得了车子；事件$B$为最初的选择是车子。易得：
$$
Pr\left( A \right) =\begin{cases}
Pr\left( B \right) =\frac{1}{3}& \text{如果没交换}\\
Pr\left( A\cap B \right) +Pr\left( A\cap \bar{B} \right) =\frac{2}{3}& \text{如果交换了}\\
\end{cases}
$$
一个赌徒玩一个公平的赌博游戏：每一步，他掷一枚公平的硬币，如果是人头面则赢 1 分，如果不是，输 1 分。他以得分$k$开始，并将继续比赛，直到他的得分达到 0（输）或$n > k$（赢）。定义事件$A$为赌徒失败，求$Pr_k(A)$：从$k$分开始事件$A$发生的概率。
$Proof$：1、记事件$B$为第一次投掷结果为人头面；
2、由全概率公式有：
$$
Pr_k\left( A \right) =Pr_k\left( A|B \right) \cdot Pr\left( B \right) +Pr_k\left( A|\bar{B} \right) \cdot Pr\left( \bar{B} \right)
$$
3、进而可得:
$$
Pr_k\left( A \right) =\frac{1}{2}\cdot Pr_k\left( A|B \right) +\frac{1}{2}\cdot Pr_k\left( A|\bar{B} \right)
$$
$$
=\frac{1}{2}\cdot Pr_{k+1}\left( A \right) +\frac{1}{2}\cdot Pr_{k-1}\left( A \right)
$$
4、展开有：
$$
\frac{1}{2}\cdot Pr_k\left( A \right) +\frac{1}{2}\cdot Pr_k\left( A \right) =\frac{1}{2}\cdot Pr_{k+1}\left( A \right) +\frac{1}{2}\cdot Pr_{k-1}\left( A \right)
$$
$$
\frac{1}{2}\cdot Pr_{k+1}\left( A \right) -\frac{1}{2}\cdot Pr_k\left( A \right) =\frac{1}{2}\cdot Pr_k\left( A \right) -\frac{1}{2}\cdot Pr_{k-1}\left( A \right)
$$
$$
Pr_{k+1}\left( A \right) -Pr_k\left( A \right) =Pr_k\left( A \right) -Pr_{k-1}\left( A \right)
$$
5、易得：
$$
\left\{ \begin{array}{l}
Pr_n\left( A \right) -Pr_{n-1}\left( A \right) =Pr_n\left( A \right) -Pr_{n-1}\left( A \right)\\
Pr_{n-1}\left( A \right) -Pr_{n-2}\left( A \right) =Pr_{n-2}\left( A \right) -Pr_{n-3}\left( A \right)\\
……..\\
Pr_3\left( A \right) -Pr_2\left( A \right) =Pr_2\left( A \right) -Pr_1\left( A \right)\\
Pr_2\left( A \right) -Pr_1\left( A \right) =Pr_1\left( A \right) -1\\
\end{array} \right.
$$
6、累加可得：
$$
Pr_n\left( A \right) -Pr_1\left( A \right) =\left( n-1 \right) \left( Pr_1\left( A \right) -1 \right)
$$
$$
\Downarrow
$$
$$
Pr_n\left( A \right) =Pr_1\left( A \right) +\left( n-1 \right) \left( Pr_1\left( A \right) -1 \right) =n\cdot Pr_1\left( A \right) -\left( n-1 \right) =0
$$
$$
\Downarrow
$$
$$
Pr_1\left( A \right) =1-\frac{1}{n}
$$
7、故可得：
贝叶斯公式
由条件概率公式：
$$
Pr\left( A\mid B \right) =\frac{Pr\left( A\cap B \right)}{Pr\left( B \right)}
$$
和全概率公式：
$$
Pr\left( A \right) =\sum_{i=1}^n{Pr\left( A\cap B_i \right)}=\sum_{i=1}^n{Pr\left( B_i \right) \cdot Pr\left( A\mid B_i \right)}
$$
可以得到贝叶斯公式：
$$
Pr\left( B_i\mid A \right) =\frac{Pr\left( A\cap B_i \right)}{\sum_{i=1}^n{Pr\left( A\mid B_i \right) \cdot P\left( B_i \right)}}
$$
辛普森悖论（Simpson’s Paradox）亦有人译为辛普森诡论，为英国统计学家 E.H.辛普森（E.H.Simpson）于 1951 年提出的悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。
