855学习记录之概率论样本空间与概率（3）$Ramsey$理论—— 炎泽汐$de$ Blog

文章目录[隐藏]

Union Bound（一致界）

Union Bound 即布尔不等式，对于事件$A_1,A_1,A_1,\cdot \cdot \cdot \in \varSigma $都有：

$$
Pr\left( \bigcup_{i=1}^n{A_i} \right) \le \sum_{i=1}^n{Pr\left( A_i \right)}
$$

$f$是一个$X$到$Y$的映射，若$0<\left| Y \right|<\left| X \right|$则存在$x_1,x_2\in X,x_1\ne x_2$使得$f\left( x_1 \right) =f\left( x_2 \right) $成立，通过反证法可以证明。

Ramsey 在 1928 年证明了在任何一个六个人的聚会中，至少有三个是陌生人，或者至少有三个是共同的熟人。该理论可以抽象推广为有一个$6$个点的图$G$，其补图为$\overline{G}$，则$G$或$\overline{G}$中有一个子图$K_3$（3 个节点的完全图，即一个三角形）。

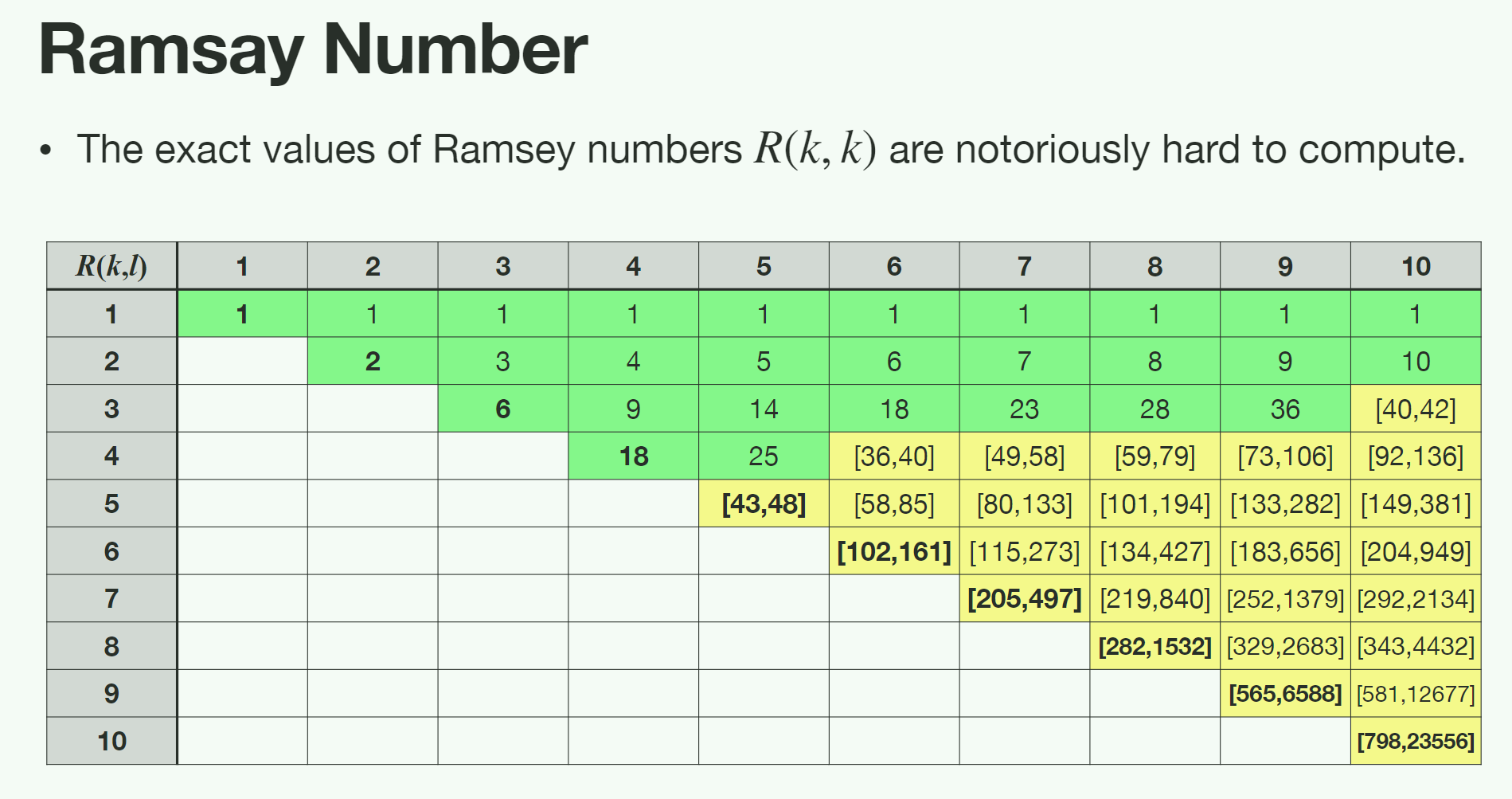
Ramsey 数是，指最小的数$n$ ，使得$n$个人中必定有$k$个人相识或$l$个人互不相识。

进一步可以推广为，Ramsey 数$n$是最小的，能够使得任何二色的$K_n$都包含两个单色且异色的子图$K_k$和$K_l$成立的正整数。

引理

如果$C_{n}^{k}\cdot 2^{1-C_{k}^{2}}<1$成立，则存在二色的$K_n$不包含单色子图$K_k$，即若$n$为使得$C_{n}^{k}\cdot 2^{1-C_{k}^{2}}<1$成立的最大数，则$R(k,k)\ge n$。

引理证明

$Proof：$1、随机地对$K_n$的边进行红蓝着色，所有边的染色相互独立，每条边等概率地被染成红色或蓝色；

2、考虑$K_n$的一个含有$k$个顶点的一个导出子图$R$，$A_R$表示事件“$R$为单色的”；

3、从$n$个顶点中选取$k$的顶点的导出子图总共有$C_{n}^{k}$种取法；

4、每个导出子图有$C_{k}^{2}$条边，故$Pr\left( A_R \right) =\frac{2}{2^{C_{k}^{2}}}=2^{1-C_{k}^{2}}$；

5、由一致界可得$Pr\left( \bigcup_R{A_R} \right) \le C_{n}^{k}\cdot 2^{1-C_{k}^{2}}$；

6、即若$C_{n}^{k}\cdot 2^{1-C_{k}^{2}}<1$成立，则存在二色的$K_n$不包含单色子图$K_k$。

引理得证！