算法
输入:待计算问题的任一实例,都需要以某种方式交给对应的算法,对所求解问题特定实例的这种描述统称为输入。
输出:经计算和处理之后得到的信息,即针对输入问题实例的答案,称作输出。
确定性和可行性是指算法可描述为由若干语义明确的基本操作组成的指令序列,且每一基本操作在对应的计算模型中均可兑现。用现代化的语言来说,一个算法满足确定性和可行性,当且仅当它可以通过程序设计语言精确地描述。
任意算法都应在执行有限次基本操作之后终止并给出输出,此即所谓算法的有穷性;进一步,算法不仅应该迟早会终止,而且所给的输出还应该能够符合由问题本身在事先决定的条件,此即算法的正确性。
证明有穷性和正确性的一个技巧就是从适当的角度审视整个计算过程,并找出其过程中的某种不变性和单调性。其中的单调性通常指问题的规模会随着算法的不断推进而递减。
不变性则不仅应在算法初始状态下自然满足,而且应与最终的正确性相呼应——当问题有效规模缩小至 0 时,不变性应当等价于正确性。如在冒泡排序中的不变性就是指经过$k$趟排序后最大的前$k$个元素已在正确位置。
除一般性情况外,实用的算法还应能够处理各种极端的输入实例。仍以排序问题为例,极端情况下待序序列的长度可能不是正数,或者反过来长度达到或者超过系统支持的最大值,或者 A[]中的元素不见得互异甚至全体相等,以上种种都属于所谓的退化情况。算法所谓的鲁棒性,就是要求能够尽可能充分地应对此类情况。
从实用角度评判不同算法及其不同实现方式时,可采用的另一标准是: 算法的总体框架能否便捷地推广至其它场合。算法模式可推广并适用于不同类型基本元素的这种特性,即是重用性的一种典型形式。
算法效率
计算效率——复杂度度量
在评价算法运行效率时往往可以忽略其处理小规模问题时的能力差异,转而关注其在处理更大规模问题时的表现。其中的原因不难理解,小规模问题所需的处理时间本来就相对更少,故此时不同算法的实际效率差异并不明显;而在处理更大规模的问题时,效率的些许差异都将对实际执行效果产生巨大的影响。这种着眼长远、更为注重时间复杂度的总体变化趋势和增长速度的策略与方法,即所谓的渐进分析。
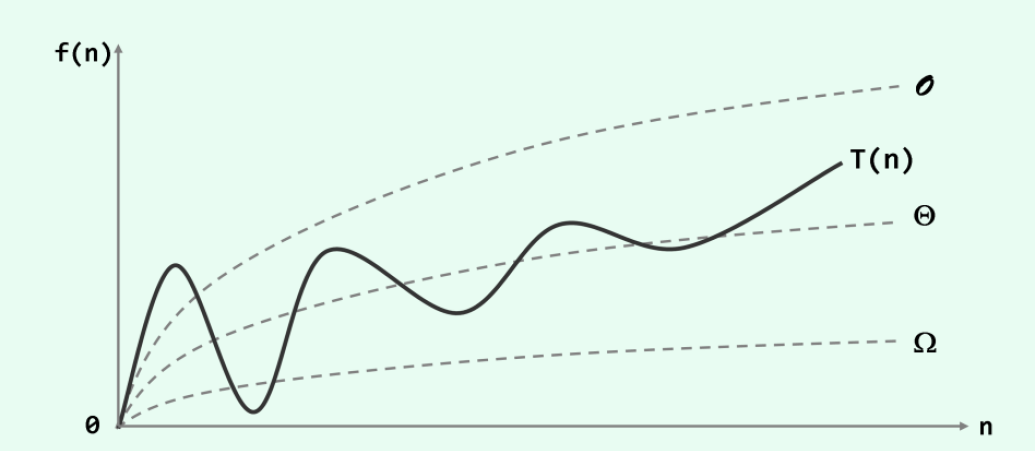
常用的渐进复杂度包括三种记号:
$$
\left\{ \begin{array}{l}
\text{大}O\text{记号:渐进上界,保守估计}\\
\text{大}\varOmega \text{记号:渐进下界,最好估计}\\
\text{大}\varTheta \text{记号:精确估计}\\
\end{array} \right.
$$
除了执行时间的长短,算法所需存储空间的多少也是衡量其性能的一个重要方面,此即所谓的空间复杂度。实际上,以上针对时间复杂度所引入的几种渐进记号,也适用于对空间复杂度的度量,其原理及方法基本相同。
需要注意的是,为了更为客观地评价算法性能的优劣,除非特别申明,空间复杂度通常并不计入原始输入本身所占用的空间。对于同一问题,这一指标对任何算法都是相同的。反之,其它(如转储、中转、索引、映射、缓冲等)各个方面所消耗的空间,则都应计入。
另外,很多时候都更多地甚至仅仅关注于算法的时间复杂度,而不必对空间复杂度做专门的考查。这种简便评测方式的依据,来自于以下事实:就渐进复杂度的意义而言,在任一算法的任何一次运行过程中所消耗的存储空间,都不会多于其间所执行基本操作的累计次数。
数据结构
数据结构是数据项的结构化集合,其结构性表现为数据项之间的相互联系及作用,也可以理解为定义于数据项之间的某种逻辑次序。根据这种逻辑次序的复杂程度,大致可以将各种数据结构划分为线性结构、半线性结构与非线性结构三大类。
$$
\text{线性结构的存取方法}\left\{ \begin{array}{l}
\text{直接存取结构(随机访问)}\\
\text{顺序存取结构}\\
\text{字典结构}\\
\end{array} \right.
$$
$$
\text{非线性结构关系类型}\left\{ \begin{array}{l}
\text{层次结构}\\
\text{群结构(无顺序关系)}\\
\end{array} \right.
$$
$$
\text{数据结构的存储方法}\left\{ \begin{array}{l}
\text{顺序存储方法}\\
\text{链接存储方法}\\
\text{索引存储方法}\left\{ \begin{array}{l}
\text{稠密索引}\\
\text{稀疏索引}\\
\end{array} \right.\\
\text{散列存储方法}\\
\end{array} \right.
$$
$$
\text{关系类型}\left\{ \begin{array}{l}
\text{线性:一对一}\\
\text{树形:一对多}\\
\text{图形:多对多}\\
\end{array} \right.
$$
$$
\text{数据结构三要素}\left\{ \begin{array}{l}
\text{逻辑结构}\\
\text{存储结构}\\
\text{操作}\\
\end{array} \right.
$$
$$
\text{抽象数据类型}\left\{ \begin{array}{l}
\text{数据抽象}\\
\text{过程抽象}\\
\end{array} \right.
$$