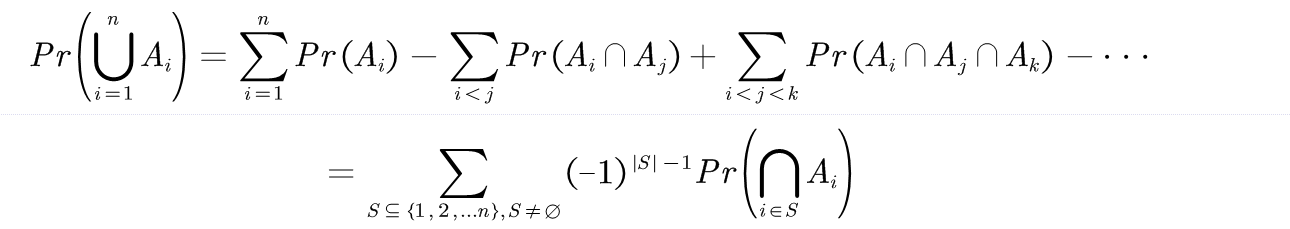855学习记录之概率论样本空间与概率（2）拓展1——炎泽汐 の Blog

文章目录[隐藏]

• Buffon’s Needle Problem (蒲丰投针问题)
• Principles of Inclusion-Exclusion（容斥原理）
• Derangement（不动点问题）
• 概率测度的连续性

      若一根长度为 $l$的短针，抛在横线间间距为$d\ge l$的均匀横纹纸上，则针落在一个与某条横线相交的位置的概率恰为$p = \frac{2l}{\pi d} $。这个结果意味着可以通过实验得到$\pi$的近似值：掷针$N$次,得到正面的结果(相交) $P$次，则$\pi$可以由逼近$ \frac{2lN}{dP} $

积分证明

---

设其落在与水平线成 $\alpha $角的位置，且 $\alpha $的取值范围是$ 0\le \alpha \le \frac{\pi}{2} $(由对称性不计斜率为负的情形，因为它与正斜率时概率相等)。

则落在斜率为$\alpha $处的针高度为$l\sin \alpha$，与间距为$d$的横线相交的概率是$\frac{l\sin \alpha}{d}$，于是对可能的角度$\alpha $取平均值，就得到概率：

$Pr\left( A \right) =\frac{2}{\pi}\cdot \int_0^{\frac{\pi}{2}}{\frac{l\sin \alpha}{d}d\alpha}\ =\ \frac{2l}{\pi d}\left[ -\cos \alpha \right] _{0}^{\frac{\pi}{2}}\ =\ \frac{2l}{\pi d}$

容斥原理：对于事件$A_1,A_1,A_1,\cdot \cdot \cdot \in \varSigma $都有：

Boole-Bonferroni Inequality 布尔邦费罗尼不等式：对于事件$A_1,A_1,A_1,\cdot \cdot \cdot \in \varSigma $，对于任意$\boldsymbol{k}\ge 0$都有：

$$
\sum_{S\subseteq \left\{ 1,2,…n \right\} ,1\le S\le 2\boldsymbol{k}}{\left( -1 \right) ^{\left| S \right|-1}Pr\left( \bigcap_{i\in S}{A_i} \right)}\le Pr\left( \bigcup_{i=1}^n{A_i} \right) \le \sum_{S\subseteq \left\{ 1,2,…n \right\} ,,1\le S\le 2\boldsymbol{k}+1}{\left( -1 \right) ^{\left| S \right|-1}Pr\left( \bigcap_{i\in S}{A_i} \right)}
$$

问题描述

---

存在一个随机的序列$\pi $，记事件$\varepsilon $为不存在不动点的概率（$\forall i\in \left[ n \right] ,\pi \left[ i \right] \ne i $），求其概率。

求解

---

令事件$A_i$为$\pi \left[ i \right] =i $，则由容斥原理可得：

$$
Pr\left( \bigcup_{i=1}^n{A_i} \right) =\sum_{k=1}^n{\sum_{S\in \left( \begin{array}{c}
\left\{ 1,2,…,n \right\}\\
k\\
\end{array} \right)}{\left( -1 \right) ^{k-1}\cdot Pr\left( \bigcap_{i\in S}{A_i} \right)}}
$$

其中：

$$
Pr\left( \bigcap_{i\in S}{A_i} \right) =\frac{\left( n-\left| S \right| \right) !}{n!}
$$

故得：

$$
Pr\left( \bigcup_{i=1}^n{A_i} \right) =\sum_{k=1}^n{C_{n}^{k}\cdot \left( -1 \right) ^{k-1}\cdot \frac{\left( n-k \right) !}{n!}}=\sum_{k=1}^n{\left( -1 \right) ^{k-1}\cdot \frac{A_{n}^{k}}{k!}\cdot \frac{\left( n-k \right) !}{n!}}=-\sum_{k=1}^n{\frac{\left( -1 \right) ^k}{k!}}
$$

综上：

$$
Pr\left( \varepsilon \right) =1-Pr\left( \bigcup_{i=1}^n{A_i} \right) =1+\sum_{k=1}^n{\frac{\left( -1 \right) ^k}{k!}}=\sum_{k=0}^n{\frac{\left( -1 \right) ^k}{k!}}
$$

$$
=\lim_{n\rightarrow \infty}\sum_{k=0}^n{\frac{\left( -1 \right) ^k}{k!}}=\lim_{x\rightarrow 0}\lim_{n\rightarrow \infty}\sum_{k=0}^n{\frac{\left( x-1 \right) ^k}{k!}}=e^{x-1}\mid_{x=0}^{}=\frac{1}{e}
$$

表述

---

假设$A_1\subseteq A_2\subseteq A_3\subseteq …$是一个递增的事件序列，令$A$为其极限，即

$$
A=\bigcup_{i=1}^{\infty}{A_i}=\lim_{i\rightarrow \infty}A_i
$$

则有：

$$
Pr\left( A \right) =\lim_{i\rightarrow \infty}Pr\left( A_i \right)
$$

证明

---

$Proof$：事件 A 可以被表示为互不相交的联合：$A=A_1\uplus \left( A_2\setminus A_1 \right) \uplus \left( A_3\setminus A_2 \right) \uplus …$，故有：

$$
Pr\left( A \right) =Pr\left( A_1 \right) +\sum_{i=1}^{\infty}{Pr\left( A_{i+1}\setminus A_i \right)} =Pr\left( A_1 \right) +\underset{n\rightarrow \infty}{\lim}\sum_{i=1}^{n-1}{\left[ Pr\left( A_{i+1} \right) -Pr\left( A_i \right) \right]} =\underset{n\rightarrow \infty}{\lim}Pr\left( A_n \right)
$$

同样的可以证明$B_1\supseteq B_2\supseteq B_3\supseteq …$是一个递减的事件序列，令$B$为其极限可以得到：

$$
Pr\left( B \right) =Pr\left( \bigcap_{i=1}^{\infty}{B_i} \right) =\lim_{i\rightarrow \infty}Pr\left( B_i \right)
$$

可以通过递增序列$B_{1}^{c}\subseteq B_{2}^{c}\subseteq B_{3}^{c}\subseteq …$来进行证明。