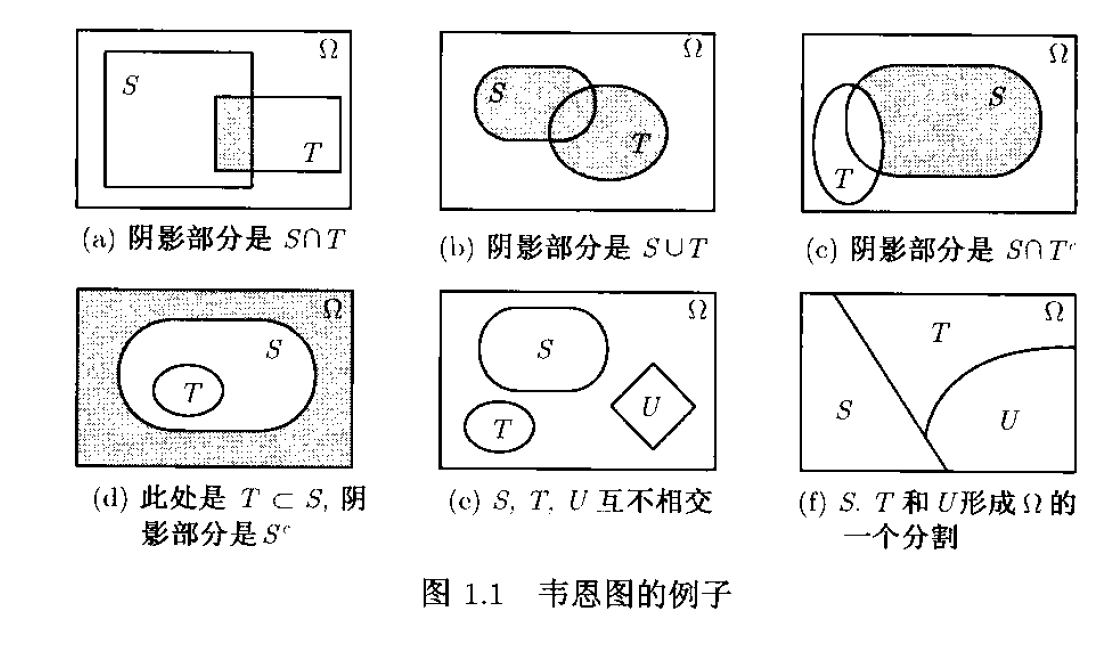
集合
概率论大量应用集合运算,集合通过将一些研究对象放在一起形成,而这些对象则称为集合的元素。将我们感趣的所有元素素放在一起形成一个集合,这个集合即为后文所称的空间。
概率模型
概率模型的基本构成包括样本空间和概率律。
样本空间
每一个概率模型都关联着一个试验,这个试验将产生一个试验结果,该试验的所有可能结果形成样本空间,用 $\varOmega $表示样本空间;样本空间的子集即某些试验结果的集合,称为事件。样本空间可由若干个试验结果组成,也可由无限多个试验结果组成。
对同一个试验根据我们的兴趣可以确定不同模型,但是对于确定模型时不能漏其样本空间中的任何一个结果,也就是说在试验过程中不管发生什么情况我们总能够得到样本空间中的一个结果。另外,在建立样本空间的时候也要避免不必要的烦琐。
概率律
概率律确定了任何结果或者任何结果的集合(称之为事件)的似然程度,更精确一点说。它给每一个事件$A$,确定一个数$P(A)$称之为事件$A$的概率它满足非负性、可加性和归一性三条公理。
概率空间的经典模型
古典概型
古典概型的定义由法国数学家拉普拉斯 (Laplace ) 提出。如果一个随机试验所包含的单位事件是有限的,且每个单位事件发生的可能性均相等,则这个随机试验叫做拉普拉斯试验,这种条件下的概率模型就叫古典概型。
在这个模型下,随机实验所有可能的结果是有限的,并且每个基本结果发生的概率是相同的。古典概型是概率论中最直观和最简单的模型,概率的许多运算规则,也首先是在这种模型下得到的。
古典概型的特点
有限性(所有可能出现的基本事件只有有限个)
等可能性(每个基本事件出现的可能性相等)
基本事件的特点
任何两个基本事件是互斥的。
任何事件(除不可能事件)都可以表示成基本事件的和。
几何概型
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积或度数)成比例,则称这样的概率模型为几何概率模型,简称为几何概型。几何概型与古典概型相对,将等可能事件的概念从有限向无限的延伸。
几何概型的特点
有限性(所有可能出现的基本事件只有有限个)
等可能性(每个基本事件出现的可能性相等)