内容大纲
855 的概率论与数一的概率论有相同点也有不同点,具体的可以去这门课程的课程主页了解,下面是传送门:
主页传送门
总的来说 855 概率论主要分为三个模块:
1、经典概率论:主要包括概率空间、随机变量及其数字特征、多维及连续随机变量、极限定理;
2、概率与计算:主要包括测度集中 (concentration of measure)、概率法 (the probabilistic method)、离散随机过程;
3、数理统计:经典与⻉叶斯统计的概念和语言(参数估计、假设检验、回归分析)。
示例问题
有偏硬币的无偏决策

原题如上,大致意思是有一个带有偏见的硬币,我们对其投掷出不同面的概率一无所知,我们应该如何使用这枚硬币以来构造两个公平的事件以进行决策呢?
这题的解答很简单,就是假设投掷到人头面的概率是$P$,那么数字面的概率就是$(1-P)$,在$P$未知的情况下如果一次一次地投掷,得到的一定是有偏的结果,故应该考虑多次投掷。如果两次两次地投掷,那么每次就有 4 种情况,其中有两种情况的概率是一致的,即先正后反和先反后正的概率均为$P*(1-P)$。这个方法将顺序作为一种无偏因素,过滤出全概率的一个子空间,从而实现公平的决策。
二孩问题
这个问题最早是在 1959 年 10 月版的《科学美国人》数学游戏专栏中提出的,具体可以表达为以下两种内容:
1、有两个孩子,老大是个男孩,两个孩子都是男孩的概率是多少?
2、有两个孩子,其中至少有一个是男孩,那么两个孩子都是男孩的概率是多少?
两个问题看似相同,实则不同。对于第一个问题,由于这两个孩子的出生是独立的,所以第二个孩子可能是男孩也可能是女孩,所以第二个孩子是男孩的概率是 1/2,于是两个孩子都是男孩的概率就是 1/2。
而对于第二个问题来说又与有所差异,从两个孩子的总样本空间来看有四种情况(1、女,女;2、女,男;3、男,女;4、男,男)。已知至少有一个是男孩则样本空间减小为三种情况(1、女,男;2、男,女;3、男,男),故两个孩子都是男孩的概率为 1/3
山羊问题
现在有三扇门 A、B、C,把一辆汽车和两头山羊等可能地放置于门后,一扇门后放一个。参赛者在三扇门中挑选一扇。他并不知道任意一扇门后面是什么。
主持人知道每扇门后面有什么。主持人从未被选择的两扇门中打开一扇放置山羊的门。参赛者会被问是否保持他的原来选择,还是转而选择剩下的那一扇门。
乍一看,开出一个山羊门后,还剩一个山羊、一辆汽车,所以换和不换的概率都是 1/2 才对。但事实并非如此,从样本空间的角度出发,由于对称性可以考虑汽车在 A 门,可以得到以下三种情况:
第一种情况:参赛者选择 A 门,主持人在 B、C 门中随便开一个,则参赛者不换就中奖,换了不中奖;
第二种情况:参赛者选择 B 门,主持人开 C 门,留 A 门,则参赛者不换不中奖,换中奖;
第三种情况:参赛者选择 C 门,主持人开门 B 门,留 A 门,则参赛者不换不中奖,换中奖。
由于参赛者不知道任意一扇门后面是什么,所有每种选择即每种情况等可能。故不换中奖的概率为 1/3,换中奖的概率为 2/3。
贝特朗悖论
贝特朗悖论是法国学者贝特朗于 1899 年针对几何概念提出的,悖论是:“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形的边长的概率是多少?”
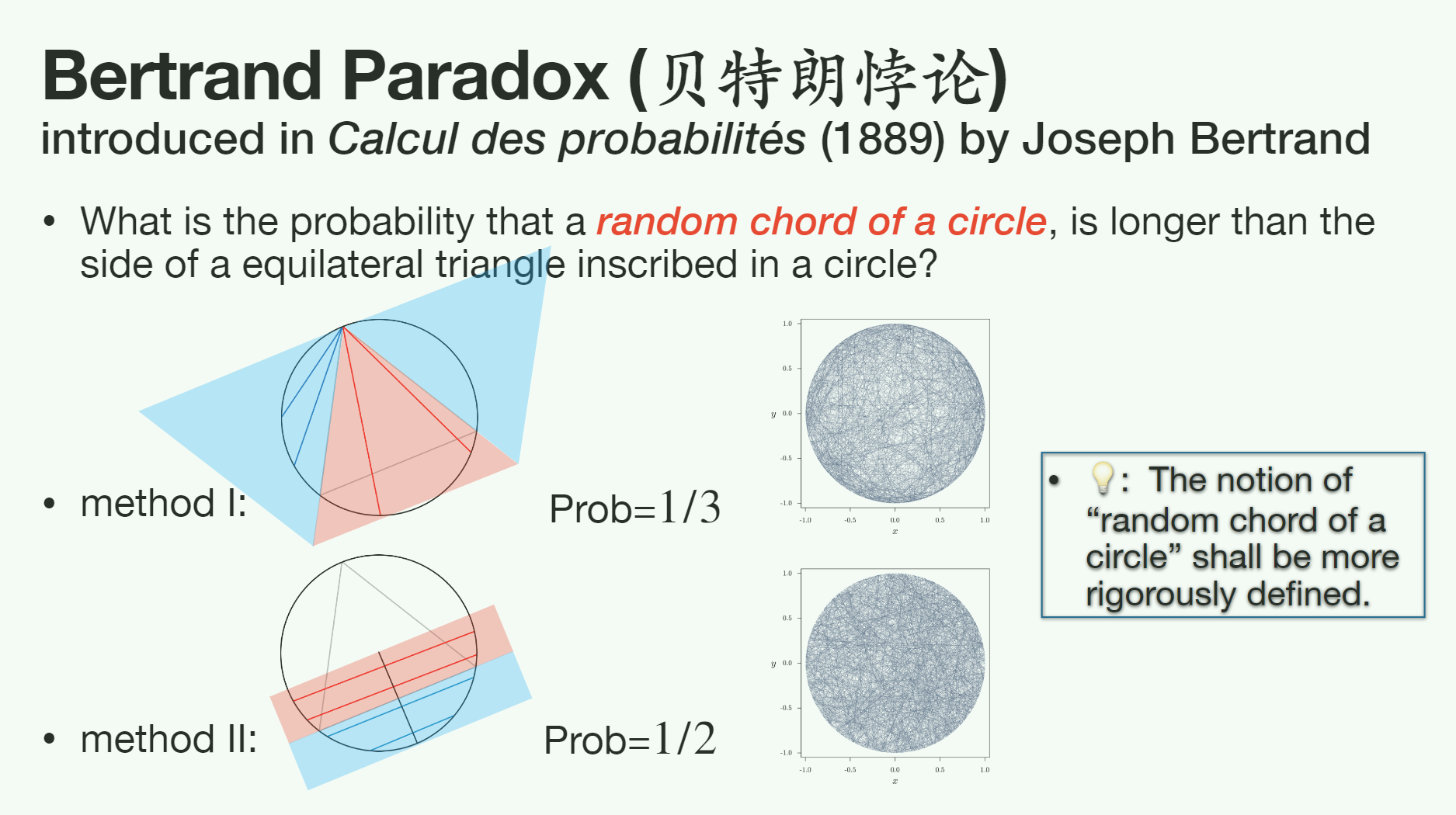
如上图所示,第一种方法假设所画弦的的一端固定在某一点上,图中将圆的内接正三角形的一个顶点 A 设为弦的出发点,弦的另一端可以落到圆周的任何位置上。
通过对图形的观察可以发现,终点落在弧 BC 上的弦的长度是一定大于正三角形的边长 L 的,而 BC 弧长占据了整个圆形周长的三分之一(放大并晃动 BC 弧),所以落在 BC 弧上的弦也占据了所有弧的 1/3。
那么这个问题就转化成了:BC 弧长占整个圆形弧长的多少,答案很简单,是 1/3。那么就可以得到结论:即,在圆内任意画弦,弦长大于正三角形边长的概率为 1/3。
第二种方法是先选择圆形的一条半径,由于对称性可以只考虑有色部分。接着过该半径上的圆心作垂线 L1,并记与等边三角形重合的弦为 L2。随后过任意点做垂线为弦,易知 L1 与 L2 之间弦长大于内接等边三角形边长,其余部分小于内接等边三角形边长。
易知 L2 与半径交点为二等分点,故可以得到结论:即,在圆内任意画弦,弦长大于正三角形边长的概率为 1/2。
贝特朗悖论产生的原因在于,古典概率中的“等概率”非常模糊:边长的分布是未知的,所以是等概率的;面积的分布是未知的,所以是等概率的。进而导出了矛盾。现代概率论通过分布来描述边长的随机性后,这种模糊性消失了,贝特朗悖论中的矛盾也就不存在的。
贝特朗悖论揭示了概率问题中对条件的选择和定义的重要性。在上面的问题中,如果我们没有明确选择线段的分布,那么答案就会有所不同。这种现象在实际应用中也很常见,比如在医学诊断中,根据不同的临床表现和检查结果可以得出不同的诊断结果。因此,在解决概率问题时,需要仔细选择和定义条件,以获得准确和有意义的答案。




